Решение дифференциальных уравнений ММС
С точки зрения численного интегрирования компонентное дифференциальное уравнение емкости С или индуктивности L может быть представлено в виде резистивной схемы (однозначно соответствующей методу интегрирования), которая поэтому и называется дискретной схемной моделью. Если обозначить значения тока І и напряжения U в текущей временной точке
Если использовать неявную формулу Эйлера, то
Найдем отсюда
Ему соответствует эквивалентная схема, изображенная на рис.6.3, которая называется дискретной моделью емкости.
Рисунок 6.3 – Дискретная схемная модель емкости
Аналогично для индуктивности. Компонентное уравнение индуктивности имеет вид:
что соответствует дискретной схемной модели индуктивности, изображенной на рис.6.4.
Рисунок 6.4 – Дискретная схемная модель индуктивности
Процесс замены дифференциальных уравнений для L и C на их резистивные схемные модели, полученные с применением неявных методов интегрирования, называется алгебраизацией дифференциальных уравнений. Таким образом, решение дифференциальных уравнений математической модели схемы (ММС) сводится к алгебраизации их на шаге интегрирования, а затем к решению полученной системы НАУ методом, например, Ньютона-Рафсона. В принципе вместо неявного метода Эйлера может быть использован любой другой неявный метод интегрирования или даже несколько методов одновременно.
|

 через
через  ,
,  , а в предыдущей точке
, а в предыдущей точке 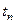 - через значения
- через значения  и
и  , то уравнение для С в дискретной форме будет иметь вид
, то уравнение для С в дискретной форме будет иметь вид . (6.8)
. (6.8) . (6.9)
. (6.9) и подставим в компонентное уравнение емкости, получим
и подставим в компонентное уравнение емкости, получим . (6.10)
. (6.10)
 . По неявной формуле Эйлера
. По неявной формуле Эйлера  . Если из одного уравнения найти
. Если из одного уравнения найти  и подставить в другое, получим
и подставить в другое, получим , (6.11)
, (6.11)



