Проблема разброса постоянных времени
Если отрезок интегрирования в рассматриваемом примере выбран небольшим [0,10], то полученное ограничение на шаг для явного метода Эйлера
Рисунок 6.6-Схема с большим разбросом постоянных времени
Однако существуют схемы с большим разбросом постоянных времени, где максимальный шаг интегрирования определяется минимальной постоянной времени, а время интегрирования – максимальной постоянной времени, во много раз большей минимальной, как в примере на рис.6.6, где решение можно записать в виде:
Такие уравнения называют жесткими. Из этих выражений видно, что переходные процессы, определяемые вторыми слагаемыми, протекают быстро и уже при t>10 они практически не сказываются на решении. При использовании явной формулы Эйлера максимальный шаг интегрирования составляет
6.8 Многошаговые методы интегрирования Более точное решение по сравнению с методами Эйлера может быть получено, если для построения интерполяционного полинома использовать не одну предыдущую точку решения Для к точек, соответствующих этим моментам времени, строится интерполяционный полином к -го порядка, посредством которого описывается кривая x(t). Для к точек Существует большое разнообразие многошаговых методов: Гира, Шихмана, Адамса – Бишофа, Милна, ФДН и т. д. Для широко используемого в программах моделирования электронных схем метода ФДН (формула дифференцирования назад) прогнозируемые значения
а наклон кривой
где Коэффициенты Гир и Брайтон показали, что формула (6.29) устойчива для Формула (6.29) применяется для решения систем ОДУ в неявной форме, т.е. в форме
Замена производной в (6.30) по формуле (6.29) приводит к системе НАУ порядка m (количество переменных) на каждом шаге интегрирования относительно Чтобы определить размер
где С другой стороны, для шагов
Если
откуда
Для выбора порядка метода интегрирования оценивается локальная ошибка Внутри каждого порядка находим
Список литературы 1. Турчак Л.И. Основы численных методов: Учебное пособие. – М.: Наука, 1987. – 320 с. 2. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: Учебное пособие. – М.: Финансы и статистика, 1999. – 256 с. 3. Норенков И.П., Маничов В.Б. Основы теории и проектирования САПР: Учеб. для втузов. – М.: Высш. шк., 1990. – 335 с. 4. Ильин В.Н. и др. Автоматизация схемотехнического проектирования: Учеб. пособие. – М.: Радио и связь, 1987. – 368 с. 5. Нарретер В. Расчет электрических цепей на ПЭВМ: Пер с нем. – М.: Энергоиздат, 1991. – 220 с. 6. Крылов и др. Вычислительные методы. Т.1. – М.: Наука, 1976. – 302 с. 7. Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. – М.: Мир, 1969.
|

 практически никак не будет влиять на выбор шага, т.к. ограничения по точности при этом более жесткие. Если отрезок интегрирования выбрать большим, например, [0,1000], то при
практически никак не будет влиять на выбор шага, т.к. ограничения по точности при этом более жесткие. Если отрезок интегрирования выбрать большим, например, [0,1000], то при  решение перестанет меняться и с точки зрения обеспечения точности решения шаг интегрирования можно увеличить. Однако, исходя из условий устойчивости, шаг интегрирования нельзя выбирать больше двух. Это приводит к большому числу шагов интегрирования.
решение перестанет меняться и с точки зрения обеспечения точности решения шаг интегрирования можно увеличить. Однако, исходя из условий устойчивости, шаг интегрирования нельзя выбирать больше двух. Это приводит к большому числу шагов интегрирования.
 ,
,  . (6.27)
. (6.27) . Полное время интегрирования будет равно (3¸5)tmax=3000¸5000нс. Потому для решения потребуется не менее 1500 шагов, хотя из соображений точности требуется на порядок меньшеe число шагов. В этом заключается проблема большого разброса постоянных времени для явных методов интегрирования. Она решается с помощью использования неявных методов интегрирования.
. Полное время интегрирования будет равно (3¸5)tmax=3000¸5000нс. Потому для решения потребуется не менее 1500 шагов, хотя из соображений точности требуется на порядок меньшеe число шагов. В этом заключается проблема большого разброса постоянных времени для явных методов интегрирования. Она решается с помощью использования неявных методов интегрирования. , а несколько. Тогда мы получим многошаговый метод численного интегрирования.
, а несколько. Тогда мы получим многошаговый метод численного интегрирования. вычисленная кривая совпадает с интерполяционным полиномом.
вычисленная кривая совпадает с интерполяционным полиномом. в т.
в т. 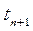 определяются по явной формуле:
определяются по явной формуле: , (6.28)
, (6.28) в этой точке, т.е.
в этой точке, т.е.  , определяется по формуле:
, определяется по формуле: , (6.29)
, (6.29)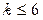 - порядок метода, который обеспечивает его устойчивость.
- порядок метода, который обеспечивает его устойчивость. и
и  определяют из совпадения решения в узловых точках со значением полинома, т.е. путём решения системы алгебраических уравнений. Однако если использовать в качестве интерполяционных многочлены Лагранжа или Ньютона, то эти коэффициенты можно вычислить аналитическим путём, что и делается в действующих программах АСхП.
определяют из совпадения решения в узловых точках со значением полинома, т.е. путём решения системы алгебраических уравнений. Однако если использовать в качестве интерполяционных многочлены Лагранжа или Ньютона, то эти коэффициенты можно вычислить аналитическим путём, что и делается в действующих программах АСхП.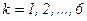 и разработали способы применения этой формулы в рамках алгоритма с автоматическим выбором шага h и порядка k в ходе интегрирования.
и разработали способы применения этой формулы в рамках алгоритма с автоматическим выбором шага h и порядка k в ходе интегрирования. . (6.30)
. (6.30) (алгебраизация дифференциальных уравнений). Поэтому объём вычислений при изменении порядка k на каждом шаге получается примерно одинаковым. Это позволяет повысить эффективность метода за счёт автоматического изменения порядка формулы (6.29) в ходе вычислений. При этом выбирается тот порядок метода, который даёт наименьшую локальную погрешность.
(алгебраизация дифференциальных уравнений). Поэтому объём вычислений при изменении порядка k на каждом шаге получается примерно одинаковым. Это позволяет повысить эффективность метода за счёт автоматического изменения порядка формулы (6.29) в ходе вычислений. При этом выбирается тот порядок метода, который даёт наименьшую локальную погрешность.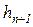 , необходимо оценить его ошибку на предыдущем шаге
, необходимо оценить его ошибку на предыдущем шаге  . На основании исследований Гира и Брайтона эту погрешность можно выразить через разность предсказанного (6.28) и вычисленного значений
. На основании исследований Гира и Брайтона эту погрешность можно выразить через разность предсказанного (6.28) и вычисленного значений  :
: , (6.31)
, (6.31)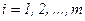 - число переменных.
- число переменных. и
и  локальные погрешности для одной переменной (i = 1) из разложения в ряд Тейлора:
локальные погрешности для одной переменной (i = 1) из разложения в ряд Тейлора: , где
, где  (6.32)
(6.32) , где
, где  (6.33)
(6.33) в диапазоне
в диапазоне  изменяется незначительно, то
изменяется незначительно, то ,
, . (6.34)
. (6.34) методов k–1, k, k+1 – порядков для каждой i -той переменной.
методов k–1, k, k+1 – порядков для каждой i -той переменной. среди
среди  находим порядок с наименьшим
находим порядок с наименьшим 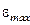 и принимаем его за
и принимаем его за  в формуле (6.34).
в формуле (6.34).



