Локальные и глобальные ошибки
В численных методах интегрирования каждый последующий шаг строится на основании результатов предыдущего. Причем на каждом шаге возникают как ошибки метода (ошибки усечения аппроксимирующего ряда), так и ошибки округления (конечность разрядной сетки ЭВМ). Различают ошибки отдельного шага вычисления (локальные) и ошибки на всем интервале интегрирования
геометрическая трактовка которого изображена на рис.6.5. Полная (глобальная) ошибка
Локальная ошибка
Рисунок 6.5 - Иллюстрация локальной и глобальной ошибок
Точность решения обычно контролируется с помощью локальной ошибки интегрирования. При этом шаг выбирается таким, чтобы локальная ошибка на этом шаге не превышала заданную величину. Если интервал времени решения заключен между
а допустимая локальная ошибка на шаге:
Тот факт, что локальная ошибка на каждом шаге не превышает ее допустимого значения, еще не гарантирует отклонения численного решения от точного на интервале интегрирования не более, чем на Уменьшая шаг интегрирования, теоретически можно получить численное решение, сколь угодно близкое к точному. Но это приведет к увеличению числа шагов интегрирования и соответственно к увеличению затрат машинного времени. Кроме того, возрастают ошибки округления. Поэтому надо стремиться получить численное решение не более точное, чем требуется.
|

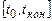 (глобальные). Исследуем проблему ошибок на тестовом примере
(глобальные). Исследуем проблему ошибок на тестовом примере , (6.19)
, (6.19)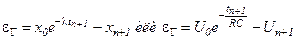 . (6.20)
. (6.20) . (6.21)
. (6.21)
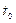 и
и 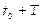 и Emax является максимально возможной ошибкой на всем интервале Т, то максимально возможная ошибка в единицу времени определяется следующим соотношением:
и Emax является максимально возможной ошибкой на всем интервале Т, то максимально возможная ошибка в единицу времени определяется следующим соотношением: , (6.22)
, (6.22)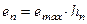 . (6.23)
. (6.23)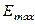 , т.к. локальные ошибки вычисляются на основании численного, а не точного решения.
, т.к. локальные ошибки вычисляются на основании численного, а не точного решения.


