Если правая часть f(t, x) и её частная производная  определены и непрерывны в некоторой области D изменения t, x, то для всякой внутренней точки (t0, х0) этой области данное уравнение имеет единственное решение, принимающее заданное значение x = x0 при
определены и непрерывны в некоторой области D изменения t, x, то для всякой внутренней точки (t0, х0) этой области данное уравнение имеет единственное решение, принимающее заданное значение x = x0 при
t = t0.
Представление дифференциального уравнения в форме Коши:
 . (6.2)
. (6.2)
Если имеется дифференциальное уравнение n -го порядка, то его можно представить в виде системы n уравнений I порядка в форме Коши.
Задача Коши.
Пусть имеется уравнение в форме Коши (6.2)

и надо найти его решение  .
.
Из теоремы Коши следует, что решение  заданного уравнения существует и единственно, если правая часть
заданного уравнения существует и единственно, если правая часть  удовлетворяет некоторым условиям гладкости (
удовлетворяет некоторым условиям гладкости ( определена и непрерывна). Будем считать, что эти условия выполнены и существует единственное решение. Будем искать решение на ряде дискретных точек t0, t1, …, tn, удаленных друг от друга на расстоянии
определена и непрерывна). Будем считать, что эти условия выполнены и существует единственное решение. Будем искать решение на ряде дискретных точек t0, t1, …, tn, удаленных друг от друга на расстоянии  , в виде
, в виде
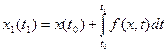 , (6.3)
, (6.3)
полученном путем интегрирования уравнения (6.2)  .
.
Если принять, что на отрезке 
 , то
, то

или, обозначив  , в дискретном виде
, в дискретном виде
 .
.
Для точки  можно записать
можно записать
 . (6.4)
. (6.4)
Полученное выражение известно как явный (прямой) метод Эйлера.
Искомая функция  на шаге интегрирования была аппроксимирована прямой, совпадающей с касательной в точке
на шаге интегрирования была аппроксимирована прямой, совпадающей с касательной в точке  (см. рис. 6.1).
(см. рис. 6.1).

Рисунок 6.1 – Иллюстрация явного метода Эйлера
В выражении (6.4) производная вычислялась в точке  . Можно также выразить
. Можно также выразить  через
через  и производную в точке
и производную в точке  , т.е.
, т.е.  . Тогда, аналогично (6.4), получим
. Тогда, аналогично (6.4), получим  .
.
Или в общем виде
 . (6.5)
. (6.5)
Эта формула называется неявным (обратным) методом Эйлера.
Можно представить (6.5) в виде 
 , где
, где  входит и в правую часть (рис. 6.2). Поэтому эта формула пригодна, когда будет предсказано значение
входит и в правую часть (рис. 6.2). Поэтому эта формула пригодна, когда будет предсказано значение  , например, с помощью явного метода Эйлера. Таким образом, мы пришли к понятию «предсказание», когда определяется значение искомой функции в последующей точке. На основе найденного «предсказания» можно рассчитать значение
, например, с помощью явного метода Эйлера. Таким образом, мы пришли к понятию «предсказание», когда определяется значение искомой функции в последующей точке. На основе найденного «предсказания» можно рассчитать значение  и использовать его при коррекции, которую выполним по неявной формуле Эйлера. Из-за ошибки «предсказания» может быть получена неточная коррекция. Чаще всего «предсказание» используется в качестве начального приближения для решения уравнения (6.5) методом Ньютона.
и использовать его при коррекции, которую выполним по неявной формуле Эйлера. Из-за ошибки «предсказания» может быть получена неточная коррекция. Чаще всего «предсказание» используется в качестве начального приближения для решения уравнения (6.5) методом Ньютона.

Рисунок 6.2 – Иллюстрация неявного метода Эйлера.
Еще одну формулу численного интегрирования можно получить, приняв  , тогда:
, тогда:
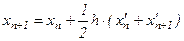 . (6.6)
. (6.6)
Это формула трапеции, которую иногда называют модифицированным методом Эйлера.
Это также неявная формула интегрирования, т. к. неизвестная величина x’n+1 входит в правую часть. Значение переменной xn+1 получают из решения нелинейного алгебраического уравнения
 (6.7)
(6.7)
методом Ньютона.
Алгоритм неявного метода Эйлера отличается от алгоритма метода трапеции отсутствием в формуле определения х составляющей  и вместо ½ h используется h.
и вместо ½ h используется h.

 определены и непрерывны в некоторой области D изменения t, x, то для всякой внутренней точки (t0, х0) этой области данное уравнение имеет единственное решение, принимающее заданное значение x = x0 при
определены и непрерывны в некоторой области D изменения t, x, то для всякой внутренней точки (t0, х0) этой области данное уравнение имеет единственное решение, принимающее заданное значение x = x0 при . (6.2)
. (6.2) .
. заданного уравнения существует и единственно, если правая часть
заданного уравнения существует и единственно, если правая часть  удовлетворяет некоторым условиям гладкости (
удовлетворяет некоторым условиям гладкости ( определена и непрерывна). Будем считать, что эти условия выполнены и существует единственное решение. Будем искать решение на ряде дискретных точек t0, t1, …, tn, удаленных друг от друга на расстоянии
определена и непрерывна). Будем считать, что эти условия выполнены и существует единственное решение. Будем искать решение на ряде дискретных точек t0, t1, …, tn, удаленных друг от друга на расстоянии  , в виде
, в виде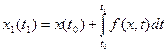 , (6.3)
, (6.3) .
.
 , то
, то
 , в дискретном виде
, в дискретном виде .
. можно записать
можно записать . (6.4)
. (6.4) на шаге интегрирования была аппроксимирована прямой, совпадающей с касательной в точке
на шаге интегрирования была аппроксимирована прямой, совпадающей с касательной в точке  (см. рис. 6.1).
(см. рис. 6.1).
 . Можно также выразить
. Можно также выразить  через
через  и производную в точке
и производную в точке  , т.е.
, т.е.  . Тогда, аналогично (6.4), получим
. Тогда, аналогично (6.4), получим  .
. . (6.5)
. (6.5)
 , где
, где  входит и в правую часть (рис. 6.2). Поэтому эта формула пригодна, когда будет предсказано значение
входит и в правую часть (рис. 6.2). Поэтому эта формула пригодна, когда будет предсказано значение  и использовать его при коррекции, которую выполним по неявной формуле Эйлера. Из-за ошибки «предсказания» может быть получена неточная коррекция. Чаще всего «предсказание» используется в качестве начального приближения для решения уравнения (6.5) методом Ньютона.
и использовать его при коррекции, которую выполним по неявной формуле Эйлера. Из-за ошибки «предсказания» может быть получена неточная коррекция. Чаще всего «предсказание» используется в качестве начального приближения для решения уравнения (6.5) методом Ньютона.
 , тогда:
, тогда: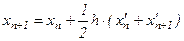 . (6.6)
. (6.6) (6.7)
(6.7) и вместо ½ h используется h.
и вместо ½ h используется h.


