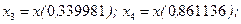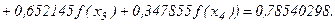Методы Чебышева и Гаусса
Все предыдущие методы имели следующую особенность: - значения х располагались равномерно, а весовые коэффициенты, в общем случае, были разными (хотя некоторые из них были равны друг другу). В методе Чебышева приняты все весовые коэффициенты одинаковыми, а хi — разными. Предварительно при использовании приведенных ниже формул метода следует преобразовать переменную интегрирования, приведя ее к диапазону [-1,1] следующим образом:
Расчетные формулы получаются для различных значений k (число ординат, использующихся при расчетах на одном участке), исходя из обеспечения возможности интегрирования без ошибки полинома как можно более высокой степени. Оказывается, можно интегрировать полином без ошибки при k = 2,3,4,5,6,7,9. Для этого уже рассчитаны необходимые параметры. Часть из них приведена ниже.
С учетом преобразования переменной формула интегрирования Чебышева будет выглядеть так:
В методе Гаусса, в отличие от метода Чебышева, все zi и все весовые коэффициенты wi — разные. Это позволило обеспечить интегрирование без ошибки уже полинома степени 2 k -1, что и для любых других, не полиномиальных подынтегральных функций дает лучшие результаты (т.е. меньшую ошибку). Некоторые значения параметров формулы интегрирования приведены ниже.
С учетом преобразования переменной формула интегрирования методом Гаусса будет выглядеть так:
Следует отметить, что в этих методах вследствие неравномерного шага интегрирования нельзя оценить погрешность интегрирования двойным просчетом. Для этой цели применяются другие достаточно сложные алгоритмы.
Пример. Рассмотрим задачу, аналогичную ранее рассмотренной в этом разделе. Для сокращения решим ее только для всего интервала сразу, не разбивая на участки. Примем k = 4. Вспоминая, что Для метода Чебышева получим:
Для метода Гаусса получим:
Если сравнить полученные результаты с аналогичными для других методов при интегрировании всего участка сразу, то можно убедиться, что последние методы обладают более высокой точностью, хотя и требуют более сложных вычислений.
|


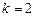 ,
, 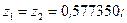
 ,
, 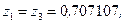
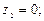
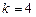 ,
, 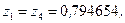
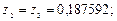
 ,
, 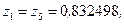
 ,
,  .
.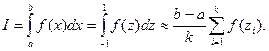

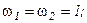

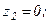
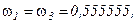
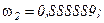
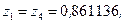

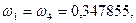
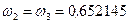 .
.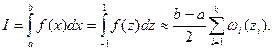
 и
и 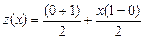 , соответственно будем иметь
, соответственно будем иметь  .
.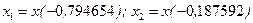 ;
;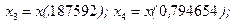

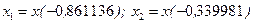 ;
;