ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
6.1 Общие сведения
Дифференциальные уравнения связаны с построением моделей динамики (движение) объектов исследования. Они описывают, как правило, изменение параметров объектов во времени (хотя могут быть и другие случаи). Результатом решения дифференциальных уравнений являются функции, а не числа, как при решении алгебраических уравнений, поэтому они и более трудоемки. При использовании численных методов решение дифференциальных уравнений представляется в табличном виде, т.е. получается совокупность значений (Xn,Yn). Решение носит шаговый характер, т.е. по одной или нескольким начальным точкам (Х,Y) за один шаг находят следующую точку, затем следующую и т.д. Решение между двумя соседними значениями аргумента Однако прежде чем обсуждать методы решения, приведем некоторые сведения из курса дифференциальных уравнений. В зависимости от числа независимых переменных, дифференциальные уравнения делятся на две категории: обыкновенные дифференциальные уравнения (ОДУ), содержащие одну независимую переменную, и уравнения с частными производными, содержащими несколько независимых переменных (например, в механике сплошных сред искомой функцией является плотность, t°, напряжение и др., а аргументами - координаты рассматриваемой точки в пространстве и время). Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции ТогдаОДУ можно записать в виде:
где t – независимая переменная. Наивысший порядок (n) производной, входящей в уравнение (6.1) называется порядком дифференциального уравнения. В частности
В ряде случаев удается выразить старшую производную в явном виде Такие уравнения называют уравнениями, разрешенными относительно старшей производной. Линейным дифференциальным уравнением называется уравнение, линейное относительно искомой функции x и её производных. Например, Решением дифференциального уравнения (6.1) n- гопорядка называется всякая функция Общее решение ОДУ n -го порядка содержит n произвольных постоянных С1, С2,, С3,,… Сn, т.е. решение ОДУ имеет вид: Частное решение ОДУ получается из общего, если произвольным постоянным задать определенные значения. Для уравнения I порядка общее решение
|

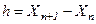 называется шагом.
называется шагом. , где х в схемотехнике – это время t, а искомая функция – х, т. е. х = f(t).
, где х в схемотехнике – это время t, а искомая функция – х, т. е. х = f(t). (6.1)
(6.1) F(t, x, x’) = 0 - дифференциальное уравнение I порядка.
F(t, x, x’) = 0 - дифференциальное уравнение I порядка. .
. - линейное уравнение.
- линейное уравнение. , которая после ее подстановки в (6.1) превращает его в тождество. Решение ОДУ может быть общим и частным.
, которая после ее подстановки в (6.1) превращает его в тождество. Решение ОДУ может быть общим и частным.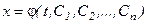 .
. , С – произвольная константа. Если положить С = С 0, тогда частное решение будет
, С – произвольная константа. Если положить С = С 0, тогда частное решение будет  .
.


