Вычислить повторные интегралы
1.

ЗАДАЧА № 23 Вычислить следующие двойные интегралы по области Д, ограниченные линиями 1.
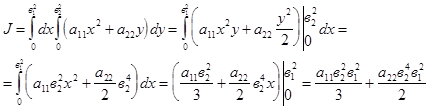
2.

=
ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПЛОСКОЙ ФИГУРЫ Площадь плоской фигуры, ограниченной областью Д, определяется по формуле Если область Д определена неравенствами а £ х £ в, j1(х) £ у £ j2(х), то двойной интеграл вычисляется по формуле Если область Д в полярных координатах определена неравенствами a £ j £ b, p1(j) £ r £ p2(j), то площадь ЗАДАЧА № 24 С помощью двойного интеграла вычислить площадь фигур 1. 1.
ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью z = f(x,y), снизу плоскостью z = 0, сбоку - цилиндрической поверхностью, вырезающей на плоскости хОу область Д, вычисляется по формуле:
ЗАДАЧА № 25 Вычислить объем тела, ограниченного заданными поверхностями 1. Проекция тела на плоскость ХОУ:
Перейдем к полярным координатам:
ПОЯСНЕНИЕ Номер варианта в задачах 9 - 25 совпадает с последней цифрой номера зачетной книжки.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ КАФЕДРА «ИНФОРМАЦИОННЫЕ СИСТЕМЫ В СТРОИТЕЛЬСТВЕ» КОНТРОЛЬНАЯ РАБОТА ПО ВЫСШЕЙ МАТЕМАТИКЕ № 1
|

 .
. .
. ; 2.
; 2.  .
. 1.
1.  ;
;  .
.
 ;
;  ;
;



 .
. .
. .
. .
. ;
;



 .
. ;
;

 .
.


