ТЕОРЕМА СУЩЕСТВОВАНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛАЕсли функция f(x) непрерывна на отрезке [ a, в ], то предел интегральной суммы существует и не зависит ни от способов разбиения на отрезке [ a, в ] на элементарные отрезки, ни от выборов точек на этих отрезках. Если функция f(x) на отрезке [ a, в ] положительна, то определенный интеграл
ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 1. 4. 4. ФОРМУЛА НЬЮТОНА - ЛЕЙБНИЦА
МЕТОДЫ ВЫЧИСЛЕНИЙ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 1. Замена переменной в интеграле Делается подстановка х = j(t) и вычисляется дифференциал dx = j¢(t)dt. Находятся новые пределы интегрирования путем решения уравнений а = j(t), в = j(t) относительно t. Тогда исходный интеграл примет вид:
2. Интегрирование по частям где U = U(x), V = V(x) - непрерывно дифференцируемые функции на [ а, в ]. ЗАДАЧА № 20 Вычислить определенный интеграл: 1.
1. 2.
ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПЛОСКОЙ ФИГУРЫ 1. Площадь криволинейной трапеции, ограниченной кривой y = f(x) [ f(x) ³ 0 ], прямыми х = а, х = в, у = 0, вычисляется по формуле
2. Площадь фигуры, ограниченной кривыми у = f1(x) и y = f2(x) сверху и снизу соответственно, вычисляется по формуле:
|
геометрически представляет собой площадь криволинейной трапеции - фигуры, ограниченной линиями
; 2. 
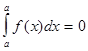; 3. 
;
;
,где F(x) - первообразная функции f(x), т.е. F¢(x) = f(x).
.
.
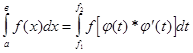; 2.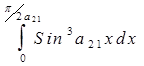 
= 
= 
.
.
