ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙРассмотрим интегралы вида:
Такие интегралы вычисляются при помощи универсальной подстановки
После подстановки интеграл примет вид Интегралы вида: Рассмотрим 2 случая. Случай 1 Хотя бы один из показателей - целое положительное нечетное число. Если положительное нечетное число n, то применяется подстановка Sinx = t, если m - нечетное положительное число, то используется подстановка Cosx = t. Случай 2 Оба показателя степени m и n - положительные четные числа. В этом случае необходимо преобразовать подынтегральную функцию с помощью формул понижения степени. ЗАДАЧА № 18 Найти неопределенный интеграл
= ЗАДАЧА № 12 Найти неопределенный интеграл
= ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Пусть функция f(x) определена на отрезке [ a, в ]. Разделим отрезок [ a, в ] на n произвольных частей точками а = х0 < х1 < х2 <... < хn-1 < хn = в. Выберем на каждом элементарном отрезке [ Xk-1, Xk ] произвольную точку Сk, обозначим длину элементарного отрезка через Интегральной суммой для функции f(x) на отрезке [ a, в ] называется сумма вида
Определение: Определенным интегралом от функции f(x) на отрезке [ a, в ] называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю
|
,где R - рациональная функция.
. Тогда 
.
где R1(t) - рациональная функция. 
.
.
.
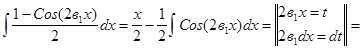
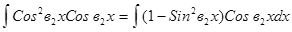
хk = xk - xk-1.
.
.
