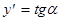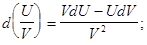Производная неявной функцииГоворят, что функция y = f(x) задана неявно, если она задана в виде уравнения f(x, y) = 0, неразрешенного относительно у. Например, х2 + у2 = ху. Для того, чтобы вычислить а) дифференцируют левую и правую части уравнения по переменной х, при этом переменную у считают функцией от х, например, (х2 + у2)х¢ = (ху)х¢; 2= + 2у * у¢ = у + ху¢;. б) решают полученное уравнение относительно у¢;, например, 2у * у¢ - х у¢ = у + 2х; у¢ (2у - х) = у + 2х; Производная функции, заданной параметрически Говорят, что функция у = f(x) задана параметрически, если она задана в виде системы уравнений: Например, При дифференцировании функции, заданной параметрически, используют формулу Геометрический смысл производной: производная - тангенс угла наклона касательной:
Механический смысл производной: производная - мгновенная скорость тела в заданный момент времени. ДИФФЕРЕНЦИАЛ ФУНУЦИИ Дифференциалом функции y = f(x) (обозначается dy, df(x)) называется главная часть приращения функции, линейная относительно приращения аргумента. Если у функции y = f(x) существует неравная нулю производная, то d f(x) = f¢(x)Dx. Например, Основные свойства дифференциала:
|
поступают следующим образом:
.
, t - параметр.
.
