Бесконечно большая функцияПусть Если функция f(x) - бесконечно большая и f(x)¹ 0 в окрестности точки а, то Как понимать х ® + ¥;, х ® - ¥; и х ® ¥;? Будем говорить, что х ® + ¥;, если х может стать больше любого наперед заданного числа, х ® - ¥;, если х может стать меньше любого наперед заданного числа, х ® ¥;, если абсолютная величина х может стать больше любого наперед заданного числа. Свойства пределов: 1. Предел суммы функций, состоящий из конечного числа слагаемых, равен сумме пределов. 2. Предел произведения равен произведению пределов. 3. Предел частного равен частному пределов, если предел знаменателя неравен нулю. Например, если а) б) в) Неопределенности. Неопределенность Рассмотрим вычисление х2-1=(х-1)*(х+1), и подставим в выражение Рассмотрим вычисление
Замечательные пределы и следствия из них.
|
и 
в окрестности точки а, тогда функция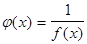 
называется бесконечно большой функцией. Обозначается 
.
.
и 
, то
;
;
.
. Подставим вместо х предельное значение 1: 
. Эта ситуация называется неопределенностью 
. Для того, чтобы вычислить 
.
. При стремлении х к бесконечности, многочлены в числителе и знаменателе стремятся к бесконечности, и возникает неопределенность вида 
. Для того, чтобы вычислить 
. 
