ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
Существуют два основных вида области интегрирования: 1.Область интегрирования Д ограничена слева и справа прямыми х = а, х = в (а < в), а снизу и сверху - непрерывными кривыми у = j1(х) и у =j2(х) (j1(х) £ j2(х)), каждая из которых пересекается прямой, параллельной оси Оу, только в одной точке (рис. 1).
Рис. 1
Рис. 2 Вычисление двойного интеграла сводится к двукратному интегрированию
Интеграл Для того, чтобы поставить пределы внутреннего интеграла, надо посмотреть на изменение у вдоль вектора 2. Пусть область интегрирования Д ограничена снизу и сверху прямыми у = с, у = d (с < d), а слева и справа - непрерывными кривыми х = Y1(у), х = Y2(у) (Y1 (у) £ Y1 (у)), каждая из которых пересекается горизонтальной прямой только в одной точке (рис. 2). Тогда двойной интеграл по такой области вычисляется по формуле
причем сначала вычисляется внутренний интеграл, ЗАДАЧА № 22
|
.
называется внутренним. В нем х считается постоянной. Этот интеграл вычисляется в первую очередь. А потом вычисляется внешний интеграл по переменной х.
от точки входа вектора в область Д (нижний предел) до точки выхода вектора из области Д (верхний предел). Пределы внешнего интеграла всегда постоянны и показывают пределы изменения переменной х.
,
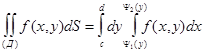, в котором у считается постоянной.
