ЧАСТНЫЕ ПРОИЗВОДНЫЕ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ.Рассмотрим функцию двух переменных z = f(x, y). Частной производной функции двух переменных z = f(x, y) по х в точке (х, у) называется предел Аналогично определяется частная производная по у в точке (х,у):
Если у функции Аналогично для переменной у: Если существует частная производная от функции В курсе высшей математики доказывается теорема о том, что если функция двух переменных определена вместе со своими частными производными в окрестности некоторой точки, причем смешанные частные производные непрерывны в этой точке, то в этом случае результат дифференцирования не зависит от порядка дифференцирования, т. е. ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ Рассмотрим функцию двух переменных z = f(x, y). Если эта функция дифференцируема в точке (х,у), то для нее существует производная по направлению любого единичного вектора ` n0 = (Cosa, Cosb), выражаемая формулой где a и b - углы, которые вектор ` n0 составляет с осями х и у. Если же необходимо найти производную по направлению произвольного вектора ` n = a`i + в`j, то его необходимо сначала пронормировать и найти направляющие косинусы по формулам
|
, если он существует. Частная производная 
есть обычная производная от функции f(x,y), рассматриваемой как функция только от переменной х при фиксированном у.
.
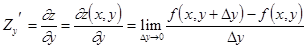. Таким образом, 
.
.
.
. 
,
а потом воспользоваться приведенной выше формулой.
