Эксергия потока вещества.
Пусть дан поток какого-либо рабочего тела с удельными параметрами торможения p, T, h, s. Эксергия потока вещества – это та максимальная работа, которую может произвести этот поток, придя в состояние равновесия с окружающей средой, параметры которой pо.с., Tо.с., hо.с., sо.с.. При этом важно не забывать, что этот переход обязательно должен быть осуществлен обратимым о бразом. Если все процессы приведения параметров потока к параметрам окружающей среды проходят обратимо, то полученная работа не зависит от выбранного пути процессов. На рис. 21 в T,s – координатах показаны возможные пути обратимого изменения параметров потока газов, который из начального состояния 1 (p, T, h, s) переходит в состояние равновесия с окружающей средой 3 (pо.с., Tо.с., hо.с., sо.с.).
Рис. 21.
Переход из 1 в 3 может быть осуществлен так:
а) изоэнтропное расширение потока от р до рО.С. (s = const) (1 – 2) и изобарный процесс отвода тепла от потока (2 – 3); б) изобарный процесс отвода тепла от потока с понижением его температуры от Т до ТО.С. (1 – 4) и изотермическое расширение потока от р до рО.С. (4 – 3); в) изотермическое расширение потока от р до рО.С. при Т= const (1 – 5) и изобарный отвод тепла от потока (5 – 3), с понижением температуры от Т до ТО.С.. Рассмотрим первый случай. Удельная эксергия потока в этом случае может быть представлена как сумма работ потока на соответствующих участках:
ex = l1-2 + l2-3
Работа изоэнтропного расширения газа:
l1-2 = h1 – h2
Работа, полученная за счет тепла изобарного процесса, не равна этому теплу, поэтому может быть представлена через коэффициент работоспособности тепла (9). Для удельных величин в дифференциальной форме:
тогда работа газа:
Т. к.
Тогда:
Сокращая h2 и учитывая, что h3 = hо.с., s3 = sо.с., s = s1 = s2, получим для суммарной работы (а значит и для эксергии):
Уравнение (11) совпадает с уравнением для эксергии потока, получаемым в курсе термодинамики, что лишний раз подтверждает правильность выбранного подхода. Стоит заметить, что последний член уравнения (11) –То.с.(s-sо.с.) имеет геометрический смысл в виде площади прямоугольника под изотермой То.с. на T,s – диаграмме (заштрихован на рис. 21). Несложный анализ этого уравнения показывает, что если температура потока остается неизменной, но меняется его давление, то это приводит к изменению величины последнего члена уравнения (11), а значит и эксергии в целом. В самом деле, если давление потока увеличивается (при Т= const), то точка 1 смещается влево и, например, в положении 1/ (р/ > р) площадь прямоугольника, а значит и последнего члена уравнения (11), уменьшается. Следовательно, эксергия потока увеличивается. При s/ = sо.с. (участок (2 – 3) стягивается в точку) ex = h – hо.с.. Снижение давления потока (при Т= const) приводит к росту энтропии потока. Точка 1 смещается вправо, площадь прямоугольника и величина То.с.(s - sо.с.) увеличивается, а эксергия – уменьшается (например, для точки 1// (p//,s//)). При некотором значении энтропии потока (точка 5) его давление становится равным давлению окружающей среды р = ро.с. (участок (1 – 2) стягивается в точку). Эксергия при этом еще остается положительной, т. к. h > hо.с. (поскольку Т > То.с.), но говорить, что работу в этом случае может совершить поток рабочего тела уже едва ли уместно, т. к. последний, в сущности, отсутствует (р = ро.с.). Работа может совершаться за счет тепла, отводимого от рабочего тела (можно говорить об эксергии тепла). Формально, при дальнейшем увеличении энтропии потока, удельная эксергия может стать равной нулю или даже отрицательной, например, в точке 1/// (p///, s///). Но, как уже отмечалось, в этих случаях говорить о потоке рабочего тела, приходящего в состояние равновесия с окружающей средой, не приходится (особенно в случае ex < 0)*.
* Случай ex = 0 тоже не может быть реализован на практике для реальных газов или пара в обозримом диапазоне температур потока (например, до 1500ºС), т. к. то, что ex = 0 означает, что h – hо.с. = То.с.(s – sо.с.). Подставляя реальные значения h и s, взятые из термодинамических таблиц для какого-либо газа или водяного пара, легко убедиться, что всегда h–hо.с. > То.с.(s–sо.с.).
|

 ,
,
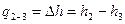 (p = const), a
(p = const), a  , то:
, то:

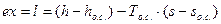 (11)
(11)


