Неопределенный интеграл и его свойства.
Неопределённый интеграл для функции f(x) - совокупность всех первообразных для функции f(x) на промежутке X Обозначается символом Свойства: 1) Производная от неопределённого интеграла равна подынтегральной функции, а дифференциал – подынтегральному выражению:
2) Определённый интеграл от производной некой функции равен самой функции + произвольная постоянная C:
3) Неопределённый интеграл от дифференциала некой функции равен этой функции + произвольная постоянная С:
4) Постоянный множитель А (А≠0) можно выносить за знак неопределённого интеграла:
5) Неопределённый интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов этих функций (если каждый из них существует):
Таблица интегралов. 8. Методы интегрирования неопределенного интеграла: непосредственное, подстановки, по частям, разложение дроби на простейшие, тригонометрических функций. 1) Непосредственное интегрирование заключается в преобразовании подынтегральной функции к табличному виду с использованием основных свойств интеграла. 2) Замена переменной (метод подстановки) в неопределённом интеграле состоит в том, что при вынесении интеграла вместо переменной х вводится новая переменная t, связанная с x определённой зависимостью x=γ(t), где γ(t) монотонна и дифференцируема, тогда справедливо равенство 3) Интегрирование по частям: если функции u= γ(u) и u=Ψ(х) непрерывно дифференцируемы на некотором промежутке, то справедлива формула:
Эта формула называется формулой интегрирования по частям. Применяется для интегрирования произведений и таких функций, как lnx, arcsinx, arccosx, степенной и тригонометрической, степенной и обратной, степенной и логарифмической и других функций. 4) Интегрирование дробей. Элементарными дробями называются дроби следующих 4-ёх типов: 1) Дробь Если
5) Интегрирование тригонометрических функций: универсальная тригонометрическая подстановка. Интеграла вида В результате подстановки: sinx= Интегралы вида 1) Один из показателей m или n – нечетное положительное число. Если n - нечетное положительное число, то подстановка sin x=t Если m - нечетное положительное число, то подстановка cos x=t 2) Оба показателя степени m и n – четные положительные числа. Надо преобразовать подынтегральную функцию с помощью формул: sinx*cosx=½sin(2x)
Интегралы вида
|

 , где С – производная постоянная, f(x) – подынтегральная функция, f(x)dx–подынтегральное выражение, х – переменная интегрирования.
, где С – производная постоянная, f(x) – подынтегральная функция, f(x)dx–подынтегральное выражение, х – переменная интегрирования.



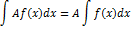
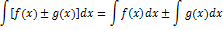


 ; 2)
; 2) 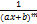 ; 3)
; 3)  ; 4)
; 4) 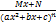 , где m, n – натуральные числа (m≥2, n≥2, b2-4ac<0)
, где m, n – натуральные числа (m≥2, n≥2, b2-4ac<0) называется правильной, если степень числителя меньше степени знаменателя, в противном случае дробь называется неправильной.
называется правильной, если степень числителя меньше степени знаменателя, в противном случае дробь называется неправильной. – правильная рациональная дробь, знаменатель P(x) которой представлен в виде линейных и квадратичных множителей P(x)=
– правильная рациональная дробь, знаменатель P(x) которой представлен в виде линейных и квадратичных множителей P(x)=  , то эта дробь может быть разложена на элементарные дроби по схеме:
, то эта дробь может быть разложена на элементарные дроби по схеме: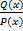 =
= 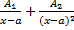 +…
+…  +…+
+…+  +
+  +…+
+…+  +
+  +
+ 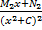 +…+
+…+  , где A1…Ak, B1 … Bp, M1…Me, N1…Nl – некоторые действительные числа. Коэффициенты Аi, Bi, Mi, Ni находят методом неопределенных коэффициентов или методом частных значений. Для этого необходимо привести равенства к общему знаменателю, приравнять коэффициенты при одинаковых степенях x в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициент и другим способом, придавая в полученном тождестве переменной х произвольное числовое значение.
, где A1…Ak, B1 … Bp, M1…Me, N1…Nl – некоторые действительные числа. Коэффициенты Аi, Bi, Mi, Ni находят методом неопределенных коэффициентов или методом частных значений. Для этого необходимо привести равенства к общему знаменателю, приравнять коэффициенты при одинаковых степенях x в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициент и другим способом, придавая в полученном тождестве переменной х произвольное числовое значение.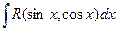 , где R – рациональная функция, приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки: tg
, где R – рациональная функция, приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки: tg 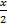 =t
=t =
= 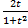 cosx=
cosx= 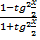 =
=  x=2arctg(t) dx=
x=2arctg(t) dx= 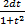
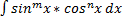
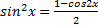

 ,
,  ,
,  . Подынтегральную функцию преобразовываем с помощью тригонометрических формул:
. Подынтегральную функцию преобразовываем с помощью тригонометрических формул:





