ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. ОСНОВНЫЕ ПОНЯТИЯ.
Дифференциальное уравнение (ДУ) – уравнение, связывающее независимую переменную х, функцию у = у(х) и ее производные и дифференциалы. F(x,y,y’,y’’…) = 0 ДУ содержи только производные и дифференциалы, а функцию у и переменную х – не обязательно. Если ДУ имеет одну независимую переменную, то оно обыкновенное ДУ Если ДУ имеет больше двух независимых переменных, то это ДУ частных производных Порядок ДУ – наивысший порядок производных, входящих в него. Общее решение – такая дифференцируемая функция у = у(х, С), которая при подстановке в уравнение обращает его в тождество. y'=y, y = cex Иногда Ф(х,у,С)=0, которое не разрешается относительно У. Тогда это общий интеграл, а не решение. Решение у=у(х, СО) получается из общего решения при определенном значении С – частное решение. Задача Коши – нахождение частного решения ДУ вида у = у(х,Со), удовлетворяющего начальным условиям у(хо) = уо. Интегральная кривая – график у = у(х) решения дифференциального уравнения, т.е график функции, удовлетворяющей этому уравнению.
17. Дифференциальные уравнения 1-го порядка с разделяющимися переменными. Дифференциальным уравнением первого порядка называется соотношение, связывающее независимую переменную, функцию и ее первую производную. Общий вид: F(x, y, y`) = 0 Уравнение разрешимое относительно y`, называется дифференциальным уравнением первого порядка, разрешенное относительно производной. y` = f(x, y). Дифференциальное уравнение первого порядка с разделяющимися переменными. Диф. уравн. 1-го порядка - уравнением с разделяющимися переменными, если оно пожжет быть представлено в виде Для решения дифференциального уравнения искомую функцию y представим в виде произведения двух множителей y = uv, где u – некоторое ненулевое решение соответствующего однородного уравнения. u` + p(x) = 0, а v-новая неизвестная функция. Так как y` = vu` + uv`, то подставляя … получим v[u`+p(x)u] + uv` = q(x) →uv`=q(x)
18. Однородные функции и однородное дифференциальное уравнение 1-го порядка. Опр. Многочлен P(x,y) = ∑aijxiyj называется однородным степени n, если все его члены имеют один и тот же порядок n, т.е. для каждого члена имеем I + j = n Если аргументы x,y однородного многочлена степени n заменить на пропорциональные величины λx и λy, то в результате этот многочлен увеличится на n-степень коэффициента пропорциональности λ. Опр. Функция P(x,y) называется однородной степени n относительно своих аргументов х и у, если для любого числа λ (кроме 0) имеет место: Р(λх, λу) = λ”P(x,y) Р. Однородным дифф. уравнением называется уравнение вида М(х,у)dx + N(x,y)dy = 0, где M(x,y) и N(x,у) – однородные функции одной и той же степени. Опр. Дифф. уравнение, которое можно преобразовать к виду y’ = ϕ( С помощью подстановки u = Действительно, y = ux, тогда y’ = u’x ≠ ux’ Подставим в y’ = ϕ(
Или: После этого осуществляется подстановка u =
|

 , где
, где 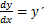
 ) называется однородным.
) называется однородным. или u=yx, где u(x) – новая неизвестная функция, данное уравнение приводится к уравнению с разделяющимися переменными.
или u=yx, где u(x) – новая неизвестная функция, данное уравнение приводится к уравнению с разделяющимися переменными.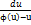 =
=  ;
; 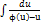 =
=  + C
+ C


