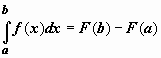СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
1) Если переставить пределы интегрирования, то изменится лишь знак:
2) Каковы бы ни были а и b, всегда имеет место равенство:
3) Постоянный множитель А выносится за знак определенного интеграла:
4) Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций:
5) Если f(x) – неотрицательная на [a;b], функция и нижний предел меньше верхнего предела (a<b), то и сам интеграл – число неотрицательное, т.е.:
Замечание: если f (x) ≤0 на [a;b] и a<b, то Если f (x) ≥0 на [a;b] и a>b имеем Если f (x) ≤0 на [a;b], то
6) Если a ≤ b, а f(x) и u·g(x) - две непрерывные функции, которые на [a, b] удовлетворяют условию f(x) ≤ g(x), то:
7) Если a ≤ b и f(x) непрерывна на [a, b], то:
8) Если m и M – наименьшее и наибольшее значения функции f(x) на отрезке [a;b], то:
9) Теорема о среднем: Если функция f(x) непрерывна на [a;b], то существует хотя бы одна точка С на этом отрезке, такая, что справедливо равенство:
Замечание: формула справедлива также для a>b, кроме a<b Если a>b, то:
Отсюда Геометрический смысл: Если f(x) >=0 на отрезке [a;b], то интеграл левой части есть площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), а правая часть – площадь прямоугольника с тем же основанием и h=f(c). Для площади криволинейной трапеции всегда есть равновеликий ей прямоугольник с тем же основанием и h, равной ординате этой кривой. 10) Определенный интеграл с одинаковыми пределами равен 0.
Определенный интеграл как функция верхнего предела: В отличие о неопределенного интеграла, определенный интеграл – это число, величина которого зависит только от пределов a и b. Если изменить верхний предел, то величина интеграла изменится. Интеграл с переменным верхним пределом есть функция своего верхнего предела Ф(х):
Теорема: производная определенного интеграла от непрерывной функции по его верхнему пределу существует и равна подынтегральной функции в верхнем пределе.
Если функция f(x) – непрерывна, то она имеет первообразную F(x), равную определенному интегралу. 11. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА (основная формула интегрального исчисления (!)) Если f(x) непрерывна на отрезке [a;b], и F(x) - некоторая первообразная функции f(x), То:
Формулу Ньютона-Лейбница обычно записывают так:
|







 ≤0
≤0 , т.е. неравенство почленно интегрируется.
, т.е. неравенство почленно интегрируется.

 , т.е. абсолютная величина интеграла не превосходит интеграла абсолютной величины подынтегральной функции.
, т.е. абсолютная величина интеграла не превосходит интеграла абсолютной величины подынтегральной функции.
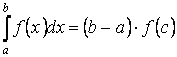

 =0
=0