Формула полной вероятности и формулы Байеса.
Формула полной вероятности: вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B 1, B 2,…, Bn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
События В1,В2,….Вn – гипотезы
Формула Байеса: пусть событие А может наступить при условии появления одного из несовместных событий B 1, B 2,…, Bn, образующих полную группу. Вероятность появления события A определяется по формуле полной вероятности:
Допустим, что испытание произведено и событие А наступило. Определим, как изменились вероятности гипотез. Другими словами, будем искать условные вероятности Согласно теореме умножения имеем:
Тогда, Используя формулу полной вероятности получаем: Она позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
34. Повторные независимые испытания: постановка задачи, формула Бернулли. Некоторые испытания называются независимыми относительно события А, если вероятность появления события А в каждом исходе не зависит от исходов других испытаний. Постановка задачи: пусть производится серия из n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р, а вероятность непоявления события А также постоянна и равна q=1-р. Тогда вероятность того, что в этой серии событие А наступит ровно k раз, равна:
Число испытаний не больше 10.
Схема Бернулли: 1)Испытание с 2 исходами 2) Испытания независимы 3)Вероятность появления события А в каждом испытании постоянна
35. Локальная теорема Муавра-Лапласа: формулировка теоремы, приближенная формула. Если испытания удовлетворяют схеме Бернулли, причем число испытаний n достаточно велико (больше 10), а вероятность появления события А в каждом испытании отлична от 0 и 1, то для вычисления вероятности появления события А в n испытаниях ровно k раз, используют приближенную формулу из локальной теоремы Муавра-Лапласа:
Функция
36. Интегральная теорема Муавра-Лапласа: формулировка теоремы, приближенная формула. Пусть испытания удовлетворяют схеме Бернулли, число испытаний n достаточно велико (больше 10), а вероятность появления события А в каждом испытании отлична от 0 и 1. Тогда для определения вероятности того, что событие А появится от k1 до k2 раз, пользуются приближенной формулой из интегральной теоремы Муавра-Лапласа:
Функция Ф(х) – нечетная, т.е. Ф(-х)= -Ф(х), значения этой функции табулированы
37. Теорема Пуассона: формулировка теоремы, приближенная формула. Если число испытаний n велико, а вероятность появления события А в каждом испытании мала (меньше 0,01), то для вычисления вероятности того, что событие А появится ровно k раз, пользуются приближенной формулой из предельной теоремы Пуассона:
Функция табулирована. Зная значения k и λ, можно сразу найти по таблице значении функции P(k, λ), которая и будет вероятностью появления события А ровно k раз в n испытаниях.
|





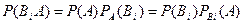
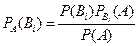

 - Формула Бернулли
- Формула Бернулли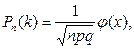 причем
причем 

 (х) – четная, т.е.
(х) – четная, т.е.  где
где ;
;  ;
; 





