Точечные и интервальные статистические оценки и их свойства.
Точечные оценки-оценки, выраженные одним числом. Пусть изучается дискретная генеральная совокупность относительно количественного признака х: 1. Генеральной средней называют среднее арифметическое значение признака генеральной совокупности. Если значения
Если значения
Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема n.
Выборочным средним Если все значения
Если значения признака
Выборочная средняя применяется для оценки неизвестного математического ожидания случайной величины. Она является несмещённой и состоятельной оценки математического ожидания. Генеральной дисперсией Dr называется среднее арифметическое квадратов отклонения значений признака х генеральной совокупности от генеральной средней.
Выборочной дисперсией Dв называется среднее арифметическое квадратов отклонения наблюдаемых значений признака Х от выборочной средней Выборочная дисперсия является состоятельной, но смещенной оценкой дисперсии. Несмещенной и состоятельной оценкой дисперсии является исправленная выборочная дисперсия
При малом объеме выборки (n<=30) пользуются исправленной выборочной дисперсией, при больших n безразлично какой пользоваться. Для практических расчетов выборочной дисперсии используют формулу:
Среднее квадратичное отклонение равно корню из выборочной дисперсии
Интервальные оценки параметров распределения определяется двумя числами – концами интервала. Интервал (Õ1; Õ2) называется доверительным для параметра О с доверительной вероятностью (надёжностью) y (0<y<1), если неравенство Õ1<O< Õ2 выполняется с вероятностью не меньше у, те P(Õ1<O< Õ2)≥y (в символе Õ еще посередине О внутри черточка, просто не нашла такой значок) Доверительный интервал для оценки неизвестного математического ожидания нормального распределения генеральной совокупности при известном среднем квадратическом отклонении вычисляется по формуле
где
|

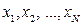 различны, то
различны, то =M(х)
=M(х) имеют соответственно частоты
имеют соответственно частоты  , причем
, причем  , то
, то =M(х)
=M(х) называют среднее арифметическое значение признака выборочной совокупности.
называют среднее арифметическое значение признака выборочной совокупности. признака выборки объема n различны, то:
признака выборки объема n различны, то: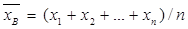 .
. имеют частоты
имеют частоты  соответственно, причем
соответственно, причем  , то:
, то: .
.

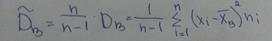


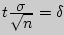 - точность оценки,
- точность оценки,  - объем выборки,
- объем выборки,  - выборочное среднее,
- выборочное среднее, 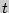 - аргумент функции Лапласа, при котором
- аргумент функции Лапласа, при котором  где α-надежность.
где α-надежность.


