Определение. Функция  , определенная и конечная на выпуклом множестве
, определенная и конечная на выпуклом множестве  называется выпуклой, если
называется выпуклой, если
 (1)
(1)
– Неравенство Йенсена.

Геометрически неравенство Йенсена означает, что если взять любые две точки графика функции и соединить их хордой, то между этими точками график функций должен лежать ниже хорды.
Определение. Функция строго выпукла, если она выпукла и ее график не содержит прямолинейных отрезков.

 – выпукла
– выпукла
 – выпукла, но не строго
– выпукла, но не строго
 – строго выпукла
– строго выпукла
Определение. Функция  называется вогнутой, если функция
называется вогнутой, если функция  выпукла.
выпукла.
Критерии выпуклости:
1) 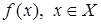 выпукла в том и только в том случае, если ее график, т.е.
выпукла в том и только в том случае, если ее график, т.е.  является выпуклым подмножеством в
является выпуклым подмножеством в  .
.
2) Скалярный критерий выпуклости. Для того чтобы функция  была выпукла, необходимо и достаточно, чтобы
была выпукла, необходимо и достаточно, чтобы  скалярная функция одной переменной
скалярная функция одной переменной  была выпуклой.
была выпуклой.
3) Гладкий критерий выпуклости. 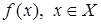 выпукла в том и только в том случае, когда выполняется неравенство:
выпукла в том и только в том случае, когда выполняется неравенство:
 (2)
(2)
4) Функция  в классе
в классе  выпукла в том и только в том случае, когда
выпукла в том и только в том случае, когда
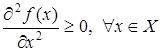 (3)
(3)
5) Если функция  ,
,  и
и  (4)
(4) 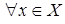 , то
, то  строго выпукла. Поскольку
строго выпукла. Поскольку  , это
, это 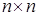 –симметрическая матрица, то для проверки (3), (4) используются критерии Сильвестра неотрицательности и положительности квадратной матрицы.
–симметрическая матрица, то для проверки (3), (4) используются критерии Сильвестра неотрицательности и положительности квадратной матрицы.
Свойства выпуклых функций:
1) Выпуклая функция непрерывна в каждой своей внутренней точке и имеет в ней производные по любому направлению.
2) Если функция  выпукла, то ее множество уровня
выпукла, то ее множество уровня  для любого конечного числа
для любого конечного числа  является либо множеством выпуклым, либо пустым.
является либо множеством выпуклым, либо пустым.
3) Если функции  выпуклы на
выпуклы на  , то и функция
, то и функция  , то и функция
, то и функция  является выпуклой.
является выпуклой.
Основная задача выпуклого программирования. Седловая точка и оптимальный план.
Рассмотрим задачу оптимизации  (1),
(1),
в которой  – вектор-функция, функции
– вектор-функция, функции  – выпуклые функции;
– выпуклые функции; 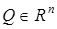 – выпуклое множество простой структуры, то есть подмножество, которое задается с помощью простейших ограничений на одну переменную (
– выпуклое множество простой структуры, то есть подмножество, которое задается с помощью простейших ограничений на одну переменную ( ). Задача называется основной задачей выпуклого программирования.
). Задача называется основной задачей выпуклого программирования.
Любая задача выпуклого программирования может быть записана в форме (1). Для этого ограничения задачи разбиваются на сложные (содержащие несколько переменных) и простые. Сложные ограничения формируют основные 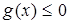 (
( – количество таких ограничений), а простые ограничения задают множество
– количество таких ограничений), а простые ограничения задают множество  . В частности, если у задачи простых ограничений нет, то полагают
. В частности, если у задачи простых ограничений нет, то полагают  . Докажем, что множество планов задачи (1) выпукло.
. Докажем, что множество планов задачи (1) выпукло.
 можно представить как
можно представить как  – выпуклое как пересечение
– выпуклое как пересечение  выпуклого множества. По параметрам задачи (1) построим функцию:
выпуклого множества. По параметрам задачи (1) построим функцию:
 , (2)
, (2)
 . Функция
. Функция  называется функцией Лагранжа для задачи (1).
называется функцией Лагранжа для задачи (1).
Определение. Пара  , где
, где
 (3)
(3)
 называется седловой точкой функции Лагранжа.
называется седловой точкой функции Лагранжа.
Теорема. Пусть известно, что 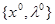 – седловая точка функции Лагранжа, тогда
– седловая точка функции Лагранжа, тогда  – оптимальный план основной задачи выпуклого программирования.
– оптимальный план основной задачи выпуклого программирования.
Доказательство. Пусть построена седловая точка. Тогда для нее выполняется неравенство (3), то есть
 (3*)
(3*)
Рассмотрим левое неравенство (3*), отбросив одинаковые константы 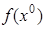 :
:
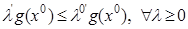 (4)
(4)
1) Докажем, что  является планом задачи (1). Поскольку известно, что
является планом задачи (1). Поскольку известно, что  , то нужно доказать, что
, то нужно доказать, что  . Предположим противное:
. Предположим противное:  . Положим в (4)
. Положим в (4)  . Тогда из (4):
. Тогда из (4): 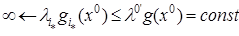 .
.  . Противоречие доказывает 1).
. Противоречие доказывает 1).
2) Докажем, что выполняются условия дополняющей не жесткости:
 . (5)
. (5)
От противного 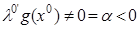 . Положим в (4)
. Положим в (4)  . Тогда
. Тогда  . Это невозможно, поскольку половина отрицательного числа всегда число большее, чем оно само.
. Это невозможно, поскольку половина отрицательного числа всегда число большее, чем оно само.
3) Докажем, что  – оптимальный план. Используем правую часть (3*):
– оптимальный план. Используем правую часть (3*):
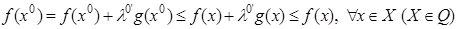 .
.  – оптимальный план для основной задачи выпуклого программирования.
– оптимальный план для основной задачи выпуклого программирования.
Ч.т.д.
Замечание. Условие оптимальности, сформулированное в теореме 1, является достаточным, но необходимым, то есть можно построить такую задачу (1), у которой существует оптимальный план, но по нему нельзя построить седловую точку для соответствующей функции Лагранжа.

 , определенная и конечная на выпуклом множестве
, определенная и конечная на выпуклом множестве  называется выпуклой, если
называется выпуклой, если (1)
(1)

 – выпукла
– выпукла – выпукла, но не строго
– выпукла, но не строго – строго выпукла
– строго выпукла выпукла.
выпукла.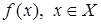 выпукла в том и только в том случае, если ее график, т.е.
выпукла в том и только в том случае, если ее график, т.е.  является выпуклым подмножеством в
является выпуклым подмножеством в  .
. скалярная функция одной переменной
скалярная функция одной переменной  была выпуклой.
была выпуклой. (2)
(2) в классе
в классе  выпукла в том и только в том случае, когда
выпукла в том и только в том случае, когда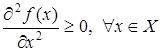 (3)
(3) и
и  (4)
(4) 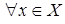 , то
, то  строго выпукла. Поскольку
строго выпукла. Поскольку  , это
, это 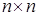 –симметрическая матрица, то для проверки (3), (4) используются критерии Сильвестра неотрицательности и положительности квадратной матрицы.
–симметрическая матрица, то для проверки (3), (4) используются критерии Сильвестра неотрицательности и положительности квадратной матрицы. выпукла, то ее множество уровня
выпукла, то ее множество уровня  для любого конечного числа
для любого конечного числа  является либо множеством выпуклым, либо пустым.
является либо множеством выпуклым, либо пустым. выпуклы на
выпуклы на  , то и функция
, то и функция  , то и функция
, то и функция  является выпуклой.
является выпуклой. (1),
(1), – вектор-функция, функции
– вектор-функция, функции  – выпуклые функции;
– выпуклые функции; 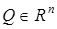 – выпуклое множество простой структуры, то есть подмножество, которое задается с помощью простейших ограничений на одну переменную (
– выпуклое множество простой структуры, то есть подмножество, которое задается с помощью простейших ограничений на одну переменную ( ). Задача называется основной задачей выпуклого программирования.
). Задача называется основной задачей выпуклого программирования.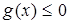 (
( – количество таких ограничений), а простые ограничения задают множество
– количество таких ограничений), а простые ограничения задают множество  . В частности, если у задачи простых ограничений нет, то полагают
. В частности, если у задачи простых ограничений нет, то полагают  . Докажем, что множество планов задачи (1) выпукло.
. Докажем, что множество планов задачи (1) выпукло. можно представить как
можно представить как  – выпуклое как пересечение
– выпуклое как пересечение  выпуклого множества. По параметрам задачи (1) построим функцию:
выпуклого множества. По параметрам задачи (1) построим функцию: , (2)
, (2) . Функция
. Функция  называется функцией Лагранжа для задачи (1).
называется функцией Лагранжа для задачи (1). , где
, где (3)
(3) называется седловой точкой функции Лагранжа.
называется седловой точкой функции Лагранжа.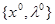 – седловая точка функции Лагранжа, тогда
– седловая точка функции Лагранжа, тогда  – оптимальный план основной задачи выпуклого программирования.
– оптимальный план основной задачи выпуклого программирования. (3*)
(3*)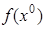 :
: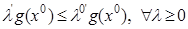 (4)
(4) , то нужно доказать, что
, то нужно доказать, что  . Предположим противное:
. Предположим противное:  . Положим в (4)
. Положим в (4)  . Тогда из (4):
. Тогда из (4): 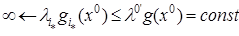 .
.  . Противоречие доказывает 1).
. Противоречие доказывает 1). . (5)
. (5)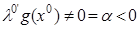 . Положим в (4)
. Положим в (4)  . Тогда
. Тогда  . Это невозможно, поскольку половина отрицательного числа всегда число большее, чем оно само.
. Это невозможно, поскольку половина отрицательного числа всегда число большее, чем оно само.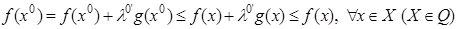 .
.  – оптимальный план для основной задачи выпуклого программирования.
– оптимальный план для основной задачи выпуклого программирования.


