Дифференцирование функций, заданных параметрически
Пусть функция (1) Требуется найти производную Имеет место формула
Пример Найти производную функции, заданной параметрически: Решение Найдем производные функций х и у по переменной t:
Согласно формуле
Исследование функций и построение графиков функций Одна из возможных схем исследования функции и построения ее графика включает следующие этапы решения задачи:
1. Найти область определения функции. 2. Найти точки пересечения графика функции с осями координат. 3. Определить четность, нечетность. 4. Найти точки разрыва функции и асимптоты графика функции. 5. Исследовать функцию на экстремум, найти интервалы монотонности функции, точки максимума и минимума. 6. Найти интервалы выпуклости, вогнутости графика функции и точки перегиба. 7. Построить график функции.
Пример С помощью методов дифференциального исчисления исследовать и построить график функции Решение 1. Область определения функции находится из условия: 2. Точки пересечения графика функции с осями координат: с осью Оу, с осью Ох, 3. Четность, нечетность. Функция В нашем случае, 4. Точки разрыва функции и асимптоты графика функции. 1) Вертикальные асимптоты. Прямая
равен Заданная функция имеет две точки разрыва второго рода
следовательно, график функции имеет две вертикальных асимптоты 2) Горизонтальные асимптоты. Горизонтальная асимптота – частный случай наклонной асимптоты, когда Чтобы найти горизонтальные асимптоты графика функции, нужно найти пределы:
Если эти пределы конечны и различны, то прямые Так как
то график функции имеет горизонтальную асимптоту
3) Наклонные асимптоты. Пусть прямая
Аналогично находится асимптота при Так как
5. Исследование функции на экстремум. Для определения интервалов возрастания и убывания функции и ее точек экстремума найдем первую производную:
Найдем критические точки, т.е. точки, в которых производная равна нулю или не существует, для чего приравниваем числитель
_ _ _ х -6 6 у
6. Исследование на выпуклость, вогнутость. Точки перегиба. Вычислим производную второго порядка:
_ + _ + х
Так как при переходе через точку
7. Построение графика функции.
|

 задана параметрически уравнениями
задана параметрически уравнениями - параметр.
- параметр. .
. или
или  .
. .
. ,
, .
. .
. .
. , т.е.
, т.е.  .
. , точка
, точка  ,
,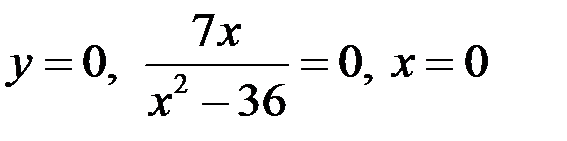 , точка
, точка  .
. называется четной, если для любого х из области определения справедливо равенство
называется четной, если для любого х из области определения справедливо равенство  . Функция
. Функция  . Если не выполнено ни одно из равенств, то функцию называют функцией общего вида.
. Если не выполнено ни одно из равенств, то функцию называют функцией общего вида. , следовательно, функция нечетная, а ее график симметричен относительно начала координат.
, следовательно, функция нечетная, а ее график симметричен относительно начала координат. является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  , если хотя бы один из пределов
, если хотя бы один из пределов или
или 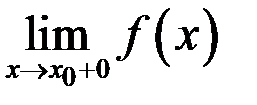
 или
или  . Таким образом, для нахождения вертикальных асимптот следует найти все точки разрыва 2-го рода данной функции. Если точек разрыва нет, то нет и вертикальных асимптот.
. Таким образом, для нахождения вертикальных асимптот следует найти все точки разрыва 2-го рода данной функции. Если точек разрыва нет, то нет и вертикальных асимптот. и
и  , так как
, так как ,
,  ,
, ,
,  ,
, и
и  .
. .
. .
. будут горизонтальными асимптотами. Если какой-либо из этих пределов не существует или равен
будут горизонтальными асимптотами. Если какой-либо из этих пределов не существует или равен  , то не существуют и соответствующие асимптоты.
, то не существуют и соответствующие асимптоты. ,
, .
.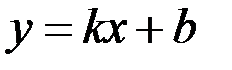 является асимптотой графика функции
является асимптотой графика функции  . Такую асимптоту называют наклонной. Для того, чтобы график функции
. Такую асимптоту называют наклонной. Для того, чтобы график функции  имел при
имел при  наклонную асимптоту
наклонную асимптоту  , необходимо и достаточно, чтобы существовали оба предела:
, необходимо и достаточно, чтобы существовали оба предела: .
. .
.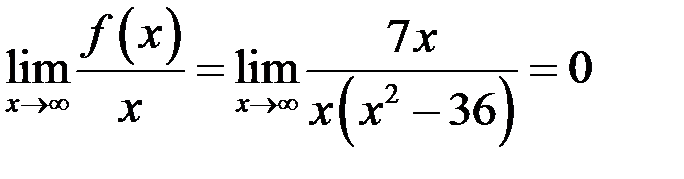 , то наклонных асимптот нет.
, то наклонных асимптот нет. .
. к нулю:
к нулю: , т.е. вещественных корней нет, следовательно, точек экстремума нет. Так как производная отрицательна во всей области определения функции, то она всюду убывает в этой области.
, т.е. вещественных корней нет, следовательно, точек экстремума нет. Так как производная отрицательна во всей области определения функции, то она всюду убывает в этой области.
 Необходимое условие точки перегиба:
Необходимое условие точки перегиба:  или не существует. Равенство
или не существует. Равенство  выполняется при
выполняется при  , следовательно, эта точка является «подозрительной» на точку перегиба. Определим знак второй производной на всей числовой оси и укажем на ней интервалы выпуклости и вогнутости функции.
, следовательно, эта точка является «подозрительной» на точку перегиба. Определим знак второй производной на всей числовой оси и укажем на ней интервалы выпуклости и вогнутости функции.
 -6
-6  0
0  6
6  у
у вторая производная меняет знак, то точка с абсциссой
вторая производная меняет знак, то точка с абсциссой  .
.



