Ранг матрицы
Пусть дана матрица
Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров. Обозначение: rang A, r (А) или r. Очевидно, Минор, порядок которого определяет ранг матрицы, называется базисным. Вычисление всех миноров отличных от нуля трудоемкая операция. На практике для вычисления r (A) используют метод Гаусса. Элементарными преобразованиями называются следующие действия над матрицами: 1. Вычеркивание нулевой строки. 2. Умножение какой либо строки на число. 3. Прибавление к одной из строк другой строки, умноженной на любое число. 4. Перестановка двух столбцов или двух строк.
Теорема 1. Ранг матрицы не меняется при элементарных преобразованиях.
Рассмотрим матрицу специального вида
в которой все «диагональные элементы»
Теорема 2. Ранг трапециевидной матрицы равен числу ее ненулевых строк.
Теорема 3. Всякую матрицу можно с помощью конечного числа элементарных преобразований привести к трапециевидному виду.
Метод Гаусса вычисления ранга матрицы состоит в приведении матрицы к трапециевидному виду и в подсчете ее ненулевых строк.
|
.
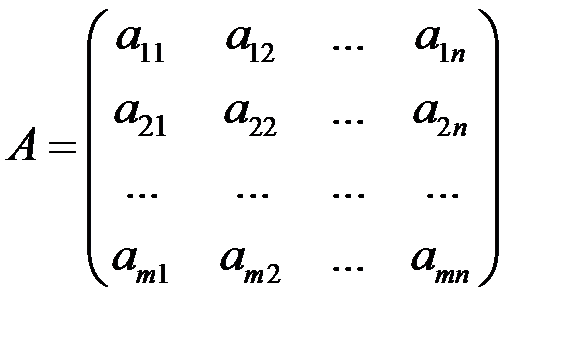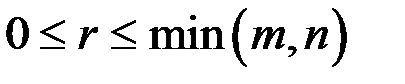– меньшее из чисел m и n.
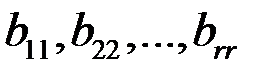отличны от нуля, а все элементы расположенные ниже диагональных, равны нулю. Такую матрицу будем называть трапециевидной. При r = n она будет треугольной.
