Условие перпендикулярности двух прямых
Две прямые перпендикулярны в том и только в том случае, когда угол j между ними равен Координаты точки
В частности, если
Если уравнение прямой дано в общей форме:
Площадь треугольника с вершинами
Пример Даны вершины треугольника 1) уравнение стороны АВ; 2) уравнение медианы, проведенной из вершины С; 3) координату точки пересечения медиан; 4) уравнение высоты, опущенной из вершины В на сторону АС и ее длину; 5) уравнение прямой, проходящей через точку С параллельно прямой АВ; 6) площадь треугольника. Решение 1) Используем уравнение прямой, проходящей через две точки
2) Медиана, проведенная из вершины С делит противолежащую сторону АВ треугольника пополам. Найдем координаты точки Е середины стороны
3) Точка М делит каждую медиану в отношении
В нашем случае
откуда 4) Найдем уравнение прямой, проходящей через заданную точку
Угловой коэффициент прямой АС равен
Длину высоты можно найти, как расстояние от точки
5) Для нахождения уравнения прямой, проходящей через точку С параллельно прямой АВ используем уравнение прямой, проходящей через заданную точку в заданном направлении
- уравнение искомой прямой. 6) Площадь треугольника находится по формуле:
у А (4;6)
Е
В (-4;0) М 0 1 х
С (-1;-4) Рис. 1
|

 , т.е.
, т.е.  .
. , делящей отрезок АВ в данном отношении
, делящей отрезок АВ в данном отношении  , где
, где  ,
,  , можно вычислить по формулам
, можно вычислить по формулам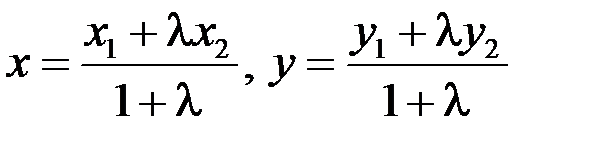 .
. , то
, то  , т.е. М – середина отрезка АВ, то формулы примут вид
, т.е. М – середина отрезка АВ, то формулы примут вид .
. , то расстояние точки
, то расстояние точки  до этой прямой находится по формуле:
до этой прямой находится по формуле: .
. ,
, 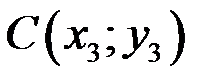 можно вычислить по формуле
можно вычислить по формуле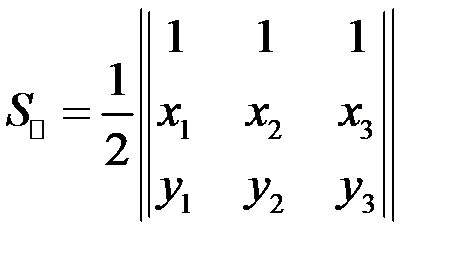 .
. . Найти:
. Найти: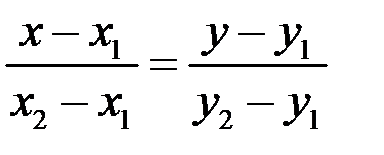 . Подставив координаты точек
. Подставив координаты точек  , получим
, получим - общее уравнение прямой АВ, из которого находим уравнение прямой с угловым коэффициентом
- общее уравнение прямой АВ, из которого находим уравнение прямой с угловым коэффициентом  ,
,  .
. (рис.1):
(рис.1): , т.е.
, т.е.  ,
,  . Подставим координаты точек в уравнение прямой, проходящей через две точки, получим
. Подставим координаты точек в уравнение прямой, проходящей через две точки, получим  - общее уравнение прямой СЕ.
- общее уравнение прямой СЕ. , считая от вершины. Таким образом, ее координаты
, считая от вершины. Таким образом, ее координаты  можно найти по формулам:
можно найти по формулам: .
. ,
, .
. перпендикулярно прямой
перпендикулярно прямой  из уравнения
из уравнения  . Найдем угловой коэффициент прямой АС, используя уравнение прямой, проходящей через две точки
. Найдем угловой коэффициент прямой АС, используя уравнение прямой, проходящей через две точки  и
и  :
: - уравнение АС.
- уравнение АС. , тогда, используя условие перпендикулярности двух прямых
, тогда, используя условие перпендикулярности двух прямых  , получим
, получим - уравнение высоты.
- уравнение высоты. до прямой АС по формуле
до прямой АС по формуле  . В нашем случае уравнение прямой АС:
. В нашем случае уравнение прямой АС:  , следовательно,
, следовательно, .
. и условие параллельности двух прямых. Известно, что угловой коэффициент прямой АВ равен
и условие параллельности двух прямых. Известно, что угловой коэффициент прямой АВ равен  , следовательно,
, следовательно, -
- , в нашем случае
, в нашем случае .
.


