Контрольная работа № 4. Интегральное исчисление функции одной переменной4.1. Найти интеграл 4.2. Найти интеграл 4.3. Найти интеграл 4.4. Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:
Краткие теоретические сведения для выполнения контрольной работы № 4 и решение типовых задач
Метод интегрирования подведением под знак дифференциала
Функция Совокупность всех первообразных для функции
Метод подведения под знак дифференциала следует из свойства инвариантности неопределенного интеграла. Пусть дан интеграл
где
Таблица интегралов
При интегрировании методом подведения под знак дифференциала необходимо иметь в виду следующие равенства:
В общем случае
Пример 1 Найти интеграл Так как
Пример 2 Найти интеграл Так как
Пример 3 Найти интеграл Так как
Пример 4 Найти интеграл Так как
|
.
.
.
, 
.
называется первообразной для функции 
на интервале 
, конечном или бесконечном, если в любой точке 
этого интервала функция 
дифференцируема и имеет производную 
.
, определенных на интервале 
, называется неопределенным интегралом от функции 
на этом интервале и обозначается символом
.
. Справедливо равенство
,
– некоторая непрерывно дифференцируемая функция.
.
.
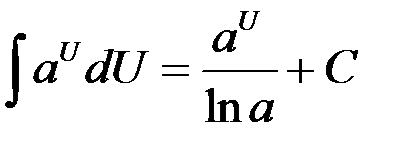
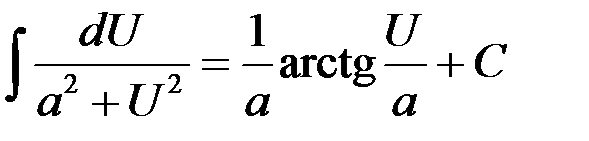
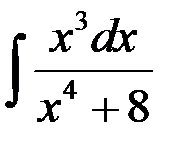, то
.
.
, то
.
.
, то
.
, то
.
