Адиабаталық процесс
Адиабаталық процесс деп жүйе мен оны қоршаған сыртқы ортаның арасында ешқандай жылу энергиясының алмасуы болмайтын процесті айтамыз. Енді термодинамиканың бірінші бастамасын ескере отырып, адиабаталық процесс кезінде газдың параметрлерін байланыстыратын теңдеуді табайық. Заттың жылу сыйымдылығы адиабаталық процесте нольге тең болады, dA = dU, (6.15) сөйтіп, сыртқы күштерге қарсы істелген жұмыс жүйенің ішкі энергиясының өзгеру әсерінен пайда болады. Бұдан адиабаталық процестің изотермалық процеске қарсы өтетінін байқаймыз. Егер (79) теңдеуге 15 – параграфтағы мәндерін қойсақ: адиабаталық үрдіс теңдеуін газ күйі теңдеуін, Майер теңдеуін ескеріп шығарып алуға болады:
Осы табылған өрнек адиабаталық процесс кезіндегі газ күйінің теңдеуі немесе Пуассон теңдеуі деп аталады. (16) теңдеудегі γ өлшемсіз шама (адиабата көрсеткіші):
Ол Пуассон коэффициенті болып есептеледі. Адиабаталық процестің pV координаттарындағы диаграммасы гипербола қисығымен кескінделеді (12 - сурет). сонымен адиабата қисығының теңдеуі
болса, изотерма қисығының теңдеуі pV = const. 3 – суреттен адиабата қисығы изотерма қисығына қарағанда тіктеу екенін көреміз. Адиабаталық үрдіс кезінде істейтін жұмысты мына түрде жазуға болады:
Политроптық процесс (C = const). Жылу сыйымдылық тұрақты болып (C = const) қалатын процесс политроптық деп аталады. Жоғарыда қарастырылған изохоралық, изотермалық, изобаралық және адиабаталық процестер осы политроптық процестің кейбір жағдайлары болып саналады. Политроп теңдеуі Мұндағы Жылу сыйымдылық мәндері мен политроп көрсеткіштері әр түрлі процестерге байланысты таблицада көрсетілген.
dT = 0, Қайтымды және қайтымсыз үрдістер. Термодинамиканың екінші және үшінші заңдары. Қайтымды және қайтымсыз үрдістер. Тұйық үрдістер. Егер термодинамиканың бірінші бастамасы энергияның бір түрден екінші түрге өзгергенінде байқалатын сандық қатынастарды көрсетсе, екінші бастамасы осы энергияның өзгерістері қандай жағдайларда жүзеге асатынын анықтайды, яғни процестердің қандай бағытта өтуі мүмкін екенін көрсетеді. Сонымен қатар термодинамикада тепе-тең күй ұғымы сияқты, қайтымды процестер ұғымының да ролі зор. Қайтымды процесс деп кері бағытта өткізуге болатын процесті тура бағытта өткізгенде жүйе қандай күйлерден өтсе, кері бағытта сондай күйлер тізбегінен өтетін процесті айтады. Сөйтіп қайтымды процеске тек тепе-теңдік процестер жатады. Сонда қайтымды процесс әуелі бір бағытта, содан соң кері бағытта бірінен соң бірі болып отыратын тепе-тең күйлердің үздіксіз тізбегінен құрылуы, сөйтіп жүйені қоршаған денелерде ешқандай өзгеріс болмауы тиіс. Тепе-тең емес процестер әрқашанда қайтымсыз процесс, дәлдеп айтқанда нақты процестер қайтымсыз процестер болады. Олар мейлінше баяу өте отырып, қайтымды процестерге тек жуықтай алады. Тұйық процесс (цикл) деп жүйе бірсыпыра өзгерістерге үшырағаннан кейін алғашқы күйіне қайтып келетін процесті айтады. Графикте мұндай цикл тұйық қисық сызықпен кескінделеді (1 - сурет) де, орындалған жұмыс сан жағынан қисықпен қоршалған ауданға тең болады. Сонда
Әдетте, оң цикл сырттан алынған жылу мөлшерінің әсерінен периодты түрде жұмыс істейтін жылу двигательдерінде қолданса, теріс цикл сыртқы күштерге қарсы жұмыс істейтін суыту қондырғыларына қолданылады. Сөйтіп, циклді орындағаннан кейін жүйе алғашқы күйіне қайта келеді. Сондықтан күйдің кез келген функциясының, яғни ішкі энергияның толық өзгерісі нольге тең болады. Сонымен тұйық процестегі істелген толық жұмыс:
Мұндағы бірінші интеграл тұйық процестегі оң бағыттағы жұмысты анықтаса, екінші интеграл теріс бағыттағы жұмысты көрсетеді. Енді термодинамиканың бірінші бастамасын тұйық процестер үшін жазайық:
Мұндағы
(2) теңдеуді
деп жазсақ бүкіл цикл кезіндегі істелген жұмыс, сырттан алынған жылу мөлшеріне тең болатынын көреміз. Бірақ тұйық процесте жүйенің жылуды алуы да, беруі де мүмкін: немесе
|

 . Олай болса, термодинамиканың бірінші бастамасы
. Олай болса, термодинамиканың бірінші бастамасы (6.16)
(6.16) (6.17)
(6.17)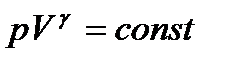
 (6.18)
(6.18)
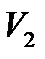


 (19)
(19) - политроп көрсеткіші деп аталады.
- политроп көрсеткіші деп аталады.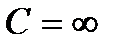



 болғандықтан изотермиялық процесс кезінде жылу сыйымдылық шексіз үлкен.
болғандықтан изотермиялық процесс кезінде жылу сыйымдылық шексіз үлкен.  болғандықтан адиабаталық процесс кезінде жылу сыйымдылық 0 – ге тең.
болғандықтан адиабаталық процесс кезінде жылу сыйымдылық 0 – ге тең. қисығы жұмыстың үлғаюын көрсетсе,
қисығы жұмыстың үлғаюын көрсетсе,  қисығы сығылуын кескіндейді. Сөйтіп
қисығы сығылуын кескіндейді. Сөйтіп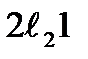 шектелген аудан ұлғаю кезіндегі істелген оң жұмысты A > 0 көрсетеді. Мұнда жұмыстың бағыты сағат тілінің бағытымен сәйкес келеді. Ал
шектелген аудан ұлғаю кезіндегі істелген оң жұмысты A > 0 көрсетеді. Мұнда жұмыстың бағыты сағат тілінің бағытымен сәйкес келеді. Ал  қисықтарымен шектелген аудан сығылу кезінде істелген теріс жұмысты кескіндейді де, бағыты сағат тілінің бағытында орындалатын циклдер оң, сғат тілінің бағытына қарсы циклдер теріс деп аталады.
қисықтарымен шектелген аудан сығылу кезінде істелген теріс жұмысты кескіндейді де, бағыты сағат тілінің бағытында орындалатын циклдер оң, сғат тілінің бағытына қарсы циклдер теріс деп аталады. (6. 19 )
(6. 19 ) (6.20)
(6.20) таңбасы интегралдың тұйық процестер үшін алынғанын көрсетеді. Ал
таңбасы интегралдың тұйық процестер үшін алынғанын көрсетеді. Ал  мөлшерін өте аз шама деп ұғамыз. Бұдан тұйық процесс кезінде ішкі энергияның өзгерісі нольге тең екенін ескеріп
мөлшерін өте аз шама деп ұғамыз. Бұдан тұйық процесс кезінде ішкі энергияның өзгерісі нольге тең екенін ескеріп


 , мұндағы
, мұндағы  - жүйенің қабылдаған,
- жүйенің қабылдаған,  - жүйенің берген жылу мөлшері. Сондықтан тұйық процесс үшін термодинамиканың пайдалы әсер коэффициенті:
- жүйенің берген жылу мөлшері. Сондықтан тұйық процесс үшін термодинамиканың пайдалы әсер коэффициенті: (6.21)
(6.21)


