Положение плоскостей в пространстве

Рассмотренные ранее положения плоскостей – не параллельные и не перпендикулярные ни к одной из плоскостей проекций – называются плоскостями общего положения.

Плоскости, перпендикулярные к одной из плоскостей проекций, называются проецирующими.

Рисунок 10 – Проецирующие плоскости

Из чертежа видно, что плоскость, перпендикулярная к плоскости проекций, составляет проекцию в виде прямой линии. Для задания проецирующих плоскостей достаточно выполнить ее одну проекцию.

Проецирующие плоскости обладают собирательным свойством – все, что находится в данной плоскости, совпадает со следом-проекцией.

 

Плоскость, заданная треугольником и на горизонтальной плоскости проекций изображается в виде прямой линии (рис. 10). Плоскости такого характера называются горизонтально-проецирующими. Плоскость, заданная параллельными прямыми m// n _┴ П₂ – фронтально-проецирующая плоскость. Проекции всех точек и прямых, лежащих в проецирующей плоскости, будут совпадать с вырожденными проекциями проецирующих плоскостей (проекция точки Р (Р₁), проекция прямой КL(К₂L₂)).

 

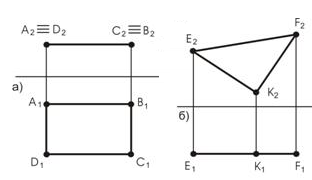Плоскости, параллельные плоскостям проекций, называются плоскостями уровня. На рисунке 11а плоскость АВСD, параллельна плоскости П₁ – горизонтальная

Рисунок 11 – Плоскости уровня

плоскость уровня.

 

Все, что находится в такой плоскости, проецируется на горизонтальную плоскость проекций в натуральную величину (без искажений). На рисунке 11б представлен треугольник ЕFК, который параллелен плоскости П₂. Следовательно, на плоскости П₂ находится проекция самого треугольника; все, что находится в треугольнике, на плоскость проекций П₂ проецируется без искажения.

 

Рисунок 13– Параллельность плоскостей

Рисунок 12 – Прямая а, парал- лельная плоскости, задан- ной плоскостью АВС