Способ плоскопараллельного перемещения
Способ плоскопараллельного перемещения – это один из способов преобразования комплексного чертежа, который основан на том, что при параллельном переносе геометрического тела относительно плоскости проекций проекция его на эту плоскость не меняет своей формы и размеров, хотя и меняет положение. При этом если точка перемещается в плоскости, параллельной П1,то ее фронтальная проекция изображается в виде прямой, параллельной оси ох (П2/П1). Если же точка перемещается в плоскости, параллельной П2, то ее горизонтальная проекция изображается в виде прямой, параллельной той же оси. Применяя способы преобразования комплексного чертежа, можно решать многие задачи, связанные с определением натуральной величины отрезков, углов, плоских фигур, а также заданием им нужного положения. 1) Определение натуральной величины отрезка прямой, занимающей общее положение (рис. 19). Для этого требуется с помощью плоскопараллельного перемещения задать прямой такое положение, чтобы она была параллельна одной из плоскостей проекций, например П2.Через произвольную точку А11,проводим прямую параллельную оси ох, и от этой точки на прямой откладываем отрезок А11 В11, равный А1В1. Из точки А11 проводим вертикальную линию связи, а из точки A2,
Новое положение фронтальной проекции точки В получим на пересечении этих линий в точке В21. После преобразования чертежа горизонтальная проекция прямой АВ стала параллельна плоскости П2, а значит, спроецировалась на эту плоскость в натуральную величину. 2) Определение натуральной величины плоскости общего положения (рис. 20). Задача решается в два этапа. На первом этапе преобразовывают чертеж так, чтобы плоскость треугольника ABC стала перпендикулярна к одной из плоскостей проекций, т.е. должна в себе содержать прямую, перпендикулярную к этой плоскости. Для этого проводят в плоскости треугольника горизонталь h
 (фронтальная проекция А212 // ох, а горизонтальная — A111). (фронтальная проекция А212 // ох, а горизонтальная — A111).
Плоскость треугольника перемещается в пространстве до тех пор, пока горизонталь h1 треугольника не станет перпендикулярна к фронтальной плоскости проекций П2.
Для этого на произвольном расстоянии от оси х вычерчивают горизонтальную проекцию треугольника A1B1C1 с условием, что А111 ┴ П2, а значит А11111 ┴ ох. При этом вершины треугольника в П1 займут новое положение – А11В11С11. Вершины треугольника в П2, перемещаясь каждая в своей плоскости //ох, займут новое положение – А21В21С21. Соединив эти точки, получают новое положение треугольника ABC, спроецированного на П2 в линию, т.е. перпендикулярного к плоскости П2. На втором этапе, чтобы получить натуральную величину треугольника ABC, его плоскость поворачивают до тех пор, пока она не будет параллельна одной из плоскостей проекций. В рассматриваемом решении фронтальную проекцию треугольника А21В21С21 располагают на произвольном расстоянии от оси х параллельно плоскости П 1, получая при этом горизонтальную плоскость уровня (ее фронтальную проекцию А22В22С22). От нового положения фронтальной проекции А22В22С22 проводят линии проекционной связи до пресечения с линиями, проведенными от точек А11В11С11 параллельно оси ох. Соединив эти точки между собой, получают треугольник ABC в натуральную величину (А12В12С12). Вопросы для самопорверки 1. Назвать способы задания плоскостей. 2. Какие положения может занимать плоскость относительно плоскостей проекций, и как она будет называться в соответствии с этим? 3. Назовите условие принадлежности прямой линии и точки плоскости. 4. Какие положения может занимать прямая линия относительно произвольной плоскости? 5. Назовите условие параллельности прямой линии и плоскости. 6. Какие этапы построения точки пересечения прямой линии и плоскости? 7. Какой случай пересечения прямой и плоскости является общим? 8. Как могут располагаться в пространстве две плоскости относительно друг друга? 9. Назовите условие параллельности плоскостей. 10. Как можно по чертежу судить о взаимной параллельности двух плоскостей? 11. В чем суть способа плоскопараллельного перемещения? 12. Как определить истинную величину прямой общего положения? 13. Какие преобразования нужно осуществить чтобы определить истинную величину плоской фигуры общего положения?
|

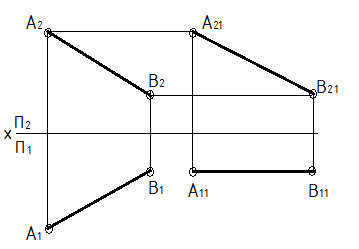 — горизонтальную линию, на пересечении которых и будет новое положение фронтальной проекции А21. Аналогично проведем вертикальную линию связи из точки В11 до пересечения с горизонтальной линией, проведенной из точки B2.
— горизонтальную линию, на пересечении которых и будет новое положение фронтальной проекции А21. Аналогично проведем вертикальную линию связи из точки В11 до пересечения с горизонтальной линией, проведенной из точки B2.


