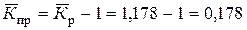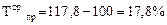Изучение развития производительных сил статистическими методами
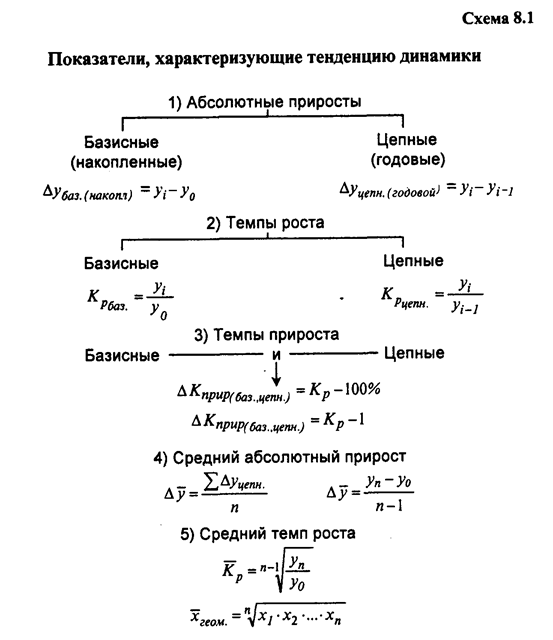
В методической второй главе курсовой работы необходимо рассмотреть методы изучения динамики статистических показателей согласно объекту исследования. Так как объектом являются производительные силы, то необходимо рассмотреть динамику как минимум трех показателей: объем производства (выполнения работ, оказания услуг), численность занятых и стоимость основных фондов. Динамика означает изменение явлений во времени. Элементами динамического ряда являются два ряда чисел: время "t" и уровень "у". Уровни обычно выражаются в виде абсолютных чисел, но иногда могут быть выражены и средними, и относительными величинами. Время может быть выражено по-разному: · на начало или конец определенного периода, т.е. на момент времени; · за определенный период времени (за месяц, квартал, год). В зависимости от характеристики времени динамические ряды бывают моментные и интервальные. Ряды динамики, где уровни характеризуют объемы явления на какие-то моменты времени, называются моментными рядами динамики. Ряды динамики, где уровни характеризуют объемы явления за какие-то периоды (месяцы, кварталы, годы), называются интервальными рядами динамики. К показателям, характеризующим тенденцию динамики, относятся следующие: - абсолютные приросты базисные (накопленные) и цепные (годовые); - темпы роста (базисные и цепные); - темпы прироста (базисные и цепные); - абсолютное значение одного процента прироста; - темп наращивания (изменения); - средний абсолютный прирост; - средний темп прироста. Для более ясного представления и использования в статистическом исследовании абсолютные и относительные показатели, выражающие динамику, представлены на схеме. Пример. Имеются следующие данные о выпуске продукции региона (в сопоставимых ценах) в 2010-2014 гг. (см. таблицу).
Таблица 9– Исходные данные
На основе приведенных данных: 1. Для анализа ряда динамики определите: 1.1. Абсолютные приросты, темпы роста и темпы прироста (цепные и базисные); 1.2. Средние: абсолютный прирост и темпы прироста. Для характеристики интенсивности динамики постройте соответствующий график. 2. Для анализа общей тенденции продажи тканей методом аналитического выравнивания: 2.1. Вычислите теоретические (выровненные) уровни и нанесите их на график, сравнив с фактическими; 2.2. Методом экстраполяции тренда рассчитайте прогноз на 2015 год. Сделайте выводы. Решение. Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными. Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными. Важнейшим статистическим показателем анализа динамики является абсолютное изменение – абсолютный прирост ( сокращение ). Абсолютное изменение характеризует увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста. Абсолютный прирост (цепной): Dyц = yi, - yi-1; Абсолютный прирост (базисный): Dyб = yi –y0, где уi — уровень сравниваемого периода; yi-1 ––– уровень предшествующего периода; у0 — уровень базисного периода. Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток, времени (SDyц = Dyб).
Рисунок 5 – Показатели, характеризующие тенденцию динамику Для характеристики интенсивности, т.е. относительного изменения уровня динамического ряда за какой-либо период времени исчисляют темпы роста (снижения). Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах — темпом роста. Эти показатели интенсивности изменения отличаются только единицами измерения. Коэффициент роста (снижения ) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число. Коэффициент роста (цепной): Коэффициент роста (базисный): Темп роста (цепной): Темп роста (базисный):
Итак, Тр =Kр×100. Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения). Темп прироста (сокращения ) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения. Темп прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах и долях единицы (коэффициенты прироста). Темп прироста (цепной): Темп прироста (базисный): Темп прироста (сокращения) можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием единицы из коэффициента роста:
Кпр = Кр – 1. (9) Результаты расчетов поместим в таблицу:
Таблица 10 – Показатели динамики
Обобщающий показатель скорости изменения уровней во времени – средний абсолютный прирост (убыль), представляющий собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний годовой абсолютный прирост как среднюю арифметическую простую:
где n – число цепных абсолютных приростов (Dyц) в изучаемом периоде. Средний темп роста (снижения) – обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления среднего темпа роста (снижения) применяется определяющий показатель – произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Следовательно, если значение признака образуется как произведение отдельных вариантов, то согласно общему правилу нужно применять среднюю геометрическую. Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах, (
где n – число цепных коэффициентов роста; Кр1ц, …, Крnц – цепные коэффициенты роста; Крб — базисный коэффициент роста за весь период. Если известны уровни динамического ряда, то расчет среднего коэффициента роста упрощается. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляется базисный коэффициент роста. Базисный коэффициент, как известно, получается непосредственно как частное от деления уровня последнего периода yn на уровень базисного периода у0. Тогда формула для расчета среднего коэффициента роста для равностоящих рядов динамики (по «базисному способу»):
где m – число уровней ряда динамики в изучаемом периоде включая базисный. Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста, вычитанием из последних 100 %. Соответственно при исчислении средних коэффициентов прироста из значений коэффициентов роста вычитается единица:
где Тср пр – средний темп прироста. Если уровни ряда динамики снижаются, то средний темп роста будет меньше 100%, а средний темп прироста – отрицательной величиной. Отрицательный темп прироста Тср пр представляет собой средний темп сокращения и характеризует среднюю относительную скорость снижения уровня. В нашей задаче: Среднегодовой коэффициент роста Среднегодовой темп роста 117,8%. Среднегодовой коэффициент прироста
Среднегодовой темп прироста
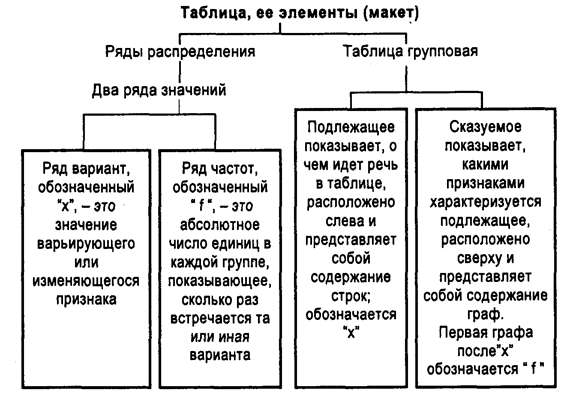
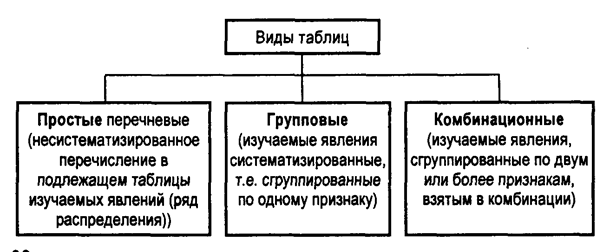
Вторая глава также основана на описании графических методов изучении динамики. Таблицы - это наиболее рациональная форма изложения результатов сводки и группировки. Подлежащее таблицы показывает, о чем идет речь в таблице, оно расположено слева и представляет собой содержание строк. Сказуемое таблицы расположено сверху и представляет собой содержание граф. Сказуемое показывает, какими признаками характеризуется подлежащее. Вид таблицы зависит от конструктивного ее построения. Существуют три вида таблиц: перечневые (простые), групповые и комбинационные. Перечневая таблица представляет собой несистематизированное перечисление в подлежащем таблицы изучаемых явлений. Если изучаемые явления систематизированы, т.е. сгруппированы по одному признаку, то получим групповую статистическую таблицу. Комбинационными, или комбинированными, называются таблицы, в которых в подлежащем дана группировка единиц совокупности по двум и более признакам, взятым в комбинации. В таблицах должно быть заглавие, указаны единицы измерения именованных показателей, подсчитаны итоги. Заглавие таблицы - это краткое пояснение основного содержания статистической сводки. На схеме кратко изображены основные положения оформления таблиц.
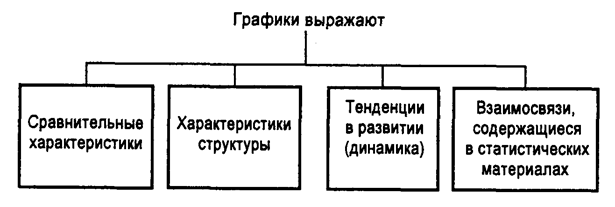
Рисунок 6 – Виды и элементы таблиц Итоговым этапом сводки и группировки статистических данных является построение графиков на основании имеющихся таблиц. Графиками называют условное, наглядное изображение статистических величин и их соотношений при помощи геометрических линий и фигур.
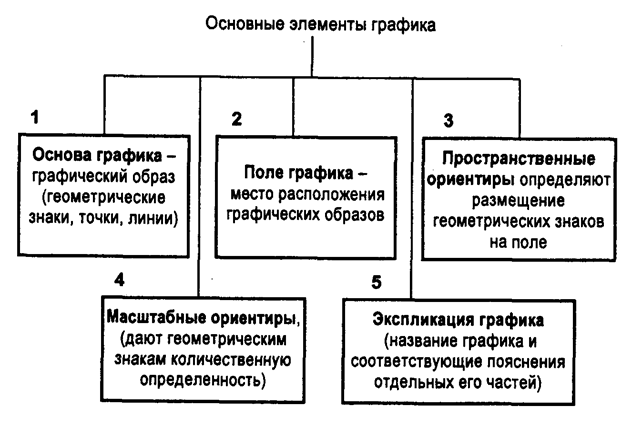
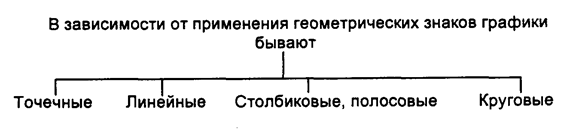
Рисунок 7 - Виды и элементов графиков
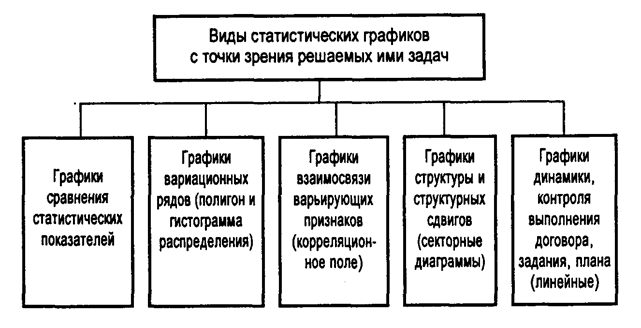
Рисунок 8 – Виды статистических графиков
Для построения графиков используют систему прямоугольных координат: ось абсцисс - периоды, варианты; ось ординат - уровни, частоты. На оси координат наносят масштабы; необходимо правильно их выбрать, чтобы графики расположились в центре поля. Динамика чаще всего изображается в виде линейного графика, непрерывной линии, характеризующей непрерывность процесса. Структура явления изображается в виде круговой и секторной диаграммы.
|

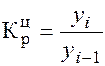 (2)
(2)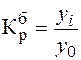 (3)
(3)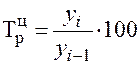 (4)
(4)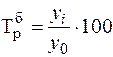 (5)
(5)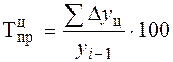 (6)
(6)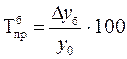 (7)
(7)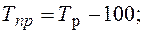 (8)
(8)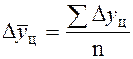 , (10)
, (10)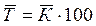 ), то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):
), то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):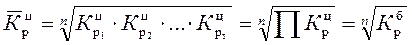 , (11)
, (11)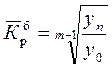 , (12)
, (12)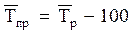 , (13)
, (13)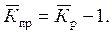 (14)
(14)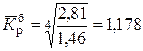 . (15)
. (15)