1. Является ли данная функция 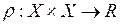 а) полуметрикой;
а) полуметрикой;
б) метрикой на данном множестве Х?
Пример 1.  - пространство интегрируемых по мере Лебега функций на отрезке [ a, b ],
- пространство интегрируемых по мере Лебега функций на отрезке [ a, b ],  .
.
Решение. Проверим выполнение аксиом полуметрики (метрики). Справедливость аксиом 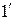 ) и 2) очевидна. С другой стороны, если
) и 2) очевидна. С другой стороны, если
 ,
,
то в силу одного из свойств интеграла Лебега (какого?) отсюда следует лишь, что 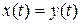 п. в. (относительно меры Лебега), а потому свойство 1) не имеет места. Справедливость свойства 3) вытекает из следующей цепочки равенств и неравенств:
п. в. (относительно меры Лебега), а потому свойство 1) не имеет места. Справедливость свойства 3) вытекает из следующей цепочки равенств и неравенств:

Таким образом, функция  является полуметрикой, но не является метрикой.
является полуметрикой, но не является метрикой.
2. Проверить, сходится ли заданная последовательность xn точек метрического пространства X к точке a.
Пример 1.  .
.
Решение. Заметим, что 
 |
| 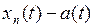 |. Так как при всех
|. Так как при всех  имеем
имеем


 при
при 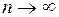 ,
,
то  при
при 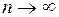 . Значит, xn сходится к a в
. Значит, xn сходится к a в  .
.
Пример 2. 
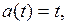
 .
.
Решение. Рассмотрим 

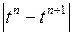 . Обозначим функцию
. Обозначим функцию  через
через  и найдем наибольшее значение функции
и найдем наибольшее значение функции 

 на отрезке
на отрезке  . Имеем
. Имеем 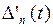
 ,
,  , если
, если  или
или  , причем
, причем  ,
,  ,
,

Значит(по правилу нахождения наибольшего значения функции на отрезке),

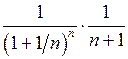

 ,
,
а потому xn сходится кточке a в пространстве  .
.
Пример 3. xn =  ,
, 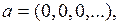
 .
.
Решение. Имеем

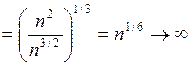 при
при 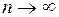 .
.
Так как  не стремится к нулю, то xn не сходится к a в l3.
не стремится к нулю, то xn не сходится к a в l3.
Пример 4. xn =  ,
,  ,
,  .
.
Решение. Имеем



 при
при 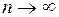 .
.
Значит, xn сходится к a в l2.
Пример 5.  .
.
Решение. Имеем




 .
.
Применим теорему Беппо Леви о предельном переходе под знаком интеграла. Введем обозначение 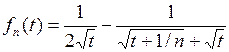 . Функция
. Функция  является интегрируемой на
является интегрируемой на  для любого
для любого  , и
, и
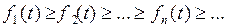 .
.
Кроме того,  .Значит, по теореме Б. Леви
.Значит, по теореме Б. Леви
 .
.
Следовательно, xn сходится к a в  .
.
Пример 6. 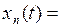
 ,
,  ,
,  .
.
Решение. Имеем




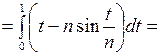


при 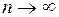 (мы воспользовались тем, что
(мы воспользовались тем, что  ~
~  при
при 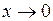 ). Значит, xn сходится к a в
). Значит, xn сходится к a в  .
.
3. Выяснить, является ли данное условие: а) необходимым, б) достаточным, в) необходимым и достаточным для сходимости последовательности xn в метрическом пространстве X?
Пример 1. 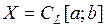 – пространство непрерывных функцийс метрикой
– пространство непрерывных функцийс метрикой 

 .
.
Условие: последовательность xn (t) поточечно сходится к непрерывной функции a (t).
Решение. Не нарушая общности, можем считать, что  . Покажем, что условие не является ни необходимым, ни достаточным. Для выяснения достаточности условия рассмотрим следующую последовательность xn (t), заданную на
. Покажем, что условие не является ни необходимым, ни достаточным. Для выяснения достаточности условия рассмотрим следующую последовательность xn (t), заданную на  графически (рисунок 6):
графически (рисунок 6):
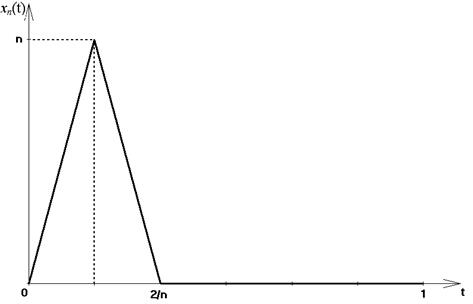
Рисунок 6 – График функции xn (t)
Последовательность xn сходится к функции 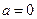 поточечно на
поточечно на  (почему?), но
(почему?), но


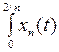

 ,
,
то есть  нестремится к нулю. Значит, данное условие не является достаточным для сходимости последовательности xn в метрическом пространстве
нестремится к нулю. Значит, данное условие не является достаточным для сходимости последовательности xn в метрическом пространстве  .
.
Теперь допустим, что  в
в 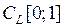 , то есть
, то есть 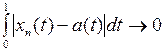 при
при 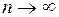 . Покажем на примере, что отсюда не следует поточечная сходимость xn к a. Рассмотримпоследовательность
. Покажем на примере, что отсюда не следует поточечная сходимость xn к a. Рассмотримпоследовательность  и функцию
и функцию 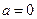 . Имеем
. Имеем
 при
при 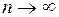 .
.
Значит,  в
в 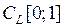 . Но последовательность
. Но последовательность  не сходится к
не сходится к  поточечно, так как
поточечно, так как  при
при  . Таким образом, данное условие не является и необходимым для сходимости последовательности xn в метрическом пространстве
. Таким образом, данное условие не является и необходимым для сходимости последовательности xn в метрическом пространстве  .
.
Пример 2.  .
.
Условие:  , где
, где 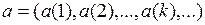 .
.
Решение. Положим  . Данное условие означает, что
. Данное условие означает, что  при
при  . Докажем, что это условие является достаточным для сходимости последовательности xn к а в пространстве
. Докажем, что это условие является достаточным для сходимости последовательности xn к а в пространстве  . Поскольку при выполнении этого условия
. Поскольку при выполнении этого условия  при достаточно больших n, то при таких n и при всех k имеем
при достаточно больших n, то при таких n и при всех k имеем 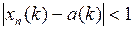 . Поэтому
. Поэтому  при этих n и при всех k. Значит,
при этих n и при всех k. Значит,
 при
при  , а это означает, что
, а это означает, что  . Следовательно,
. Следовательно,  в
в  . Достаточность доказана.
. Достаточность доказана.
Теперь покажем, что условие не является необходимым. Рассмотрим последовательность  точек из
точек из  и точку
и точку  из
из  . У нас
. У нас 
 0 при
0 при  (остаток сходящегося ряда стремится к нулю). Значит,
(остаток сходящегося ряда стремится к нулю). Значит,  в
в  . Но в этом примере
. Но в этом примере  (сравните с гармоническим рядом), а потому данное условие при
(сравните с гармоническим рядом), а потому данное условие при 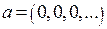 не выполняется. Наконец, если бы оно выполнялось для точки
не выполняется. Наконец, если бы оно выполнялось для точки  , то по доказанному в первой части решения было бы
, то по доказанному в первой части решения было бы  , что противоречит единственности предела.
, что противоречит единственности предела.
4. Найти предел последовательности xn в метрическом пространстве X, если он существует.
Пример 1.  .
.
Решение. 1 способ. Допустим, xn сходится к некоторой точке a в пространстве  . Так как для любого k
. Так как для любого k
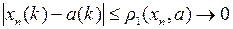 при
при  ,
,
то имеем и покоординатную сходимость xn к a. Но покоординатно xn сходится к точке

(почему?), которая не принадлежит пространству  (ряд
(ряд  расходится, по необходимому признаку). Мы пришли к противоречию. Значит, xn не сходится в
расходится, по необходимому признаку). Мы пришли к противоречию. Значит, xn не сходится в  .
.
2 способ. Так как
 при
при  ,
,
то последовательность xn не является фундаментальной в  . Следовательно, xn не сходится в
. Следовательно, xn не сходится в  .
.
Пример 2.  ,
,  .
.
Решение. 1 способ. Допустим, xn сходится к некоторому элементу a в 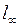 . Так как
. Так как 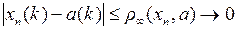 при
при  для любого k, то имеем покоординатную сходимость xn к a. Но покоординатно xn сходится к последовательности
для любого k, то имеем покоординатную сходимость xn к a. Но покоординатно xn сходится к последовательности
 ,
,
для которой  при
при  (почему?). Следовательно, xn не сходится к a в
(почему?). Следовательно, xn не сходится к a в 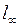 . Противоречие.
. Противоречие.
2 способ. Заметим, что последовательность xn не является фунда-ментальной в 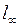 . Действительно,
. Действительно,
xn+ 1 =  ,
,
причем 
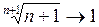 при
при  . Так как xn не фундаментальна, то она и не сходится в
. Так как xn не фундаментальна, то она и не сходится в 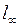 .
.

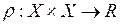 а) полуметрикой;
а) полуметрикой; - пространство интегрируемых по мере Лебега функций на отрезке [ a, b ],
- пространство интегрируемых по мере Лебега функций на отрезке [ a, b ],  .
.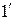 ) и 2) очевидна. С другой стороны, если
) и 2) очевидна. С другой стороны, если ,
,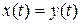 п. в. (относительно меры Лебега), а потому свойство 1) не имеет места. Справедливость свойства 3) вытекает из следующей цепочки равенств и неравенств:
п. в. (относительно меры Лебега), а потому свойство 1) не имеет места. Справедливость свойства 3) вытекает из следующей цепочки равенств и неравенств:
 является полуметрикой, но не является метрикой.
является полуметрикой, но не является метрикой. .
.
 |
| 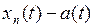 |. Так как при всех
|. Так как при всех  имеем
имеем

 при
при 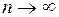 ,
, при
при  .
.
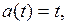
 .
.
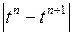 . Обозначим функцию
. Обозначим функцию  через
через  и найдем наибольшее значение функции
и найдем наибольшее значение функции 

 . Имеем
. Имеем 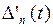
 ,
,  , если
, если  или
или  , причем
, причем  ,
,  ,
,
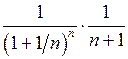

 ,
, .
. ,
, 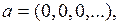
 .
.
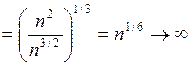 при
при  не стремится к нулю, то xn не сходится к a в l3.
не стремится к нулю, то xn не сходится к a в l3. ,
,  ,
,  .
.


 при
при  .
.



 .
.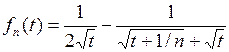 . Функция
. Функция  является интегрируемой на
является интегрируемой на  для любого
для любого  , и
, и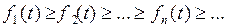 .
. .Значит, по теореме Б. Леви
.Значит, по теореме Б. Леви .
. .
.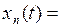
 ,
,  ,
,  .
.

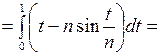


 ~
~  при
при 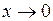 ). Значит, xn сходится к a в
). Значит, xn сходится к a в 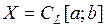 – пространство непрерывных функцийс метрикой
– пространство непрерывных функцийс метрикой 

 .
. . Покажем, что условие не является ни необходимым, ни достаточным. Для выяснения достаточности условия рассмотрим следующую последовательность xn (t), заданную на
. Покажем, что условие не является ни необходимым, ни достаточным. Для выяснения достаточности условия рассмотрим следующую последовательность xn (t), заданную на 
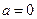 поточечно на
поточечно на 

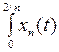
 ,
, нестремится к нулю. Значит, данное условие не является достаточным для сходимости последовательности xn в метрическом пространстве
нестремится к нулю. Значит, данное условие не является достаточным для сходимости последовательности xn в метрическом пространстве  .
. в
в 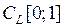 , то есть
, то есть 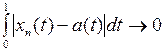 при
при  и функцию
и функцию  при
при  в
в  не сходится к
не сходится к  поточечно, так как
поточечно, так как  при
при  . Таким образом, данное условие не является и необходимым для сходимости последовательности xn в метрическом пространстве
. Таким образом, данное условие не является и необходимым для сходимости последовательности xn в метрическом пространстве  , где
, где 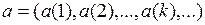 .
. . Данное условие означает, что
. Данное условие означает, что  при
при  . Докажем, что это условие является достаточным для сходимости последовательности xn к а в пространстве
. Докажем, что это условие является достаточным для сходимости последовательности xn к а в пространстве  . Поскольку при выполнении этого условия
. Поскольку при выполнении этого условия  при достаточно больших n, то при таких n и при всех k имеем
при достаточно больших n, то при таких n и при всех k имеем 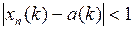 . Поэтому
. Поэтому  при этих n и при всех k. Значит,
при этих n и при всех k. Значит, при
при  . Следовательно,
. Следовательно,  в
в  точек из
точек из  из
из 
 0 при
0 при  в
в  (сравните с гармоническим рядом), а потому данное условие при
(сравните с гармоническим рядом), а потому данное условие при 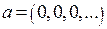 не выполняется. Наконец, если бы оно выполнялось для точки
не выполняется. Наконец, если бы оно выполнялось для точки  , то по доказанному в первой части решения было бы
, то по доказанному в первой части решения было бы  .
. . Так как для любого k
. Так как для любого k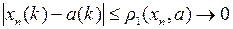 при
при 
 расходится, по необходимому признаку). Мы пришли к противоречию. Значит, xn не сходится в
расходится, по необходимому признаку). Мы пришли к противоречию. Значит, xn не сходится в  при
при  ,
,  .
.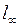 . Так как
. Так как 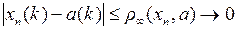 при
при  ,
, при
при  ,
,
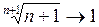 при
при 


