Всюду ниже  - метрическое пространство.
- метрическое пространство.
Определение. Пусть  .
. 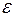 - окрестностью точки а называется открытый шар с центором в точке а радиуса
- окрестностью точки а называется открытый шар с центором в точке а радиуса 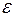 , т. е. множество
, т. е. множество
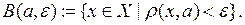
Определение. Пусть  . Точка а называется внутренней точкой множества А, если она принадлежит А вместе с некоторой своей
. Точка а называется внутренней точкой множества А, если она принадлежит А вместе с некоторой своей 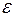 -окрестностью.
-окрестностью.
Определение. Множество всех внутренних точек множества А обозначается  и называется внутренностью множества А.
и называется внутренностью множества А.
Определение. Множество  называется открытым, если каждая его точка внутренняя.
называется открытым, если каждая его точка внутренняя.
Определение. Множество  называется замкнутым, если его дополнение
называется замкнутым, если его дополнение 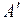 открыто.
открыто.
Определение. Пусть  . Наименьшее замкнутое множество, содержащее А, называется замыканием множества А и обозначается
. Наименьшее замкнутое множество, содержащее А, называется замыканием множества А и обозначается 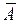 (или
(или  ).
).
Теорема (о принадлежности замыканию). Пусть  . Следующие утверждения равносильны:
. Следующие утверждения равносильны:
1)  ;
;
2)  для любого
для любого  ;
;
3)  для некоторой последовательности
для некоторой последовательности 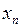 точек множества А.
точек множества А.
Определение. Если точка  удовлетворяет условию 2) (или, что равносильно, 3)) предыдущей теоремы, то она называется точкой прикосновения множества А.
удовлетворяет условию 2) (или, что равносильно, 3)) предыдущей теоремы, то она называется точкой прикосновения множества А.
Следствие. Замыкание множества А равняется объединению множества А и множества его точек прикосновения.
Определение. Границей множества А называется множество
 .
.
Точки границы называются граничными точками множества А.
Определение. Множество  называется ограниченым, если оно содержится в некотором шаре.
называется ограниченым, если оно содержится в некотором шаре.
2.2.1. Является ли данное множество Т открытым, замкнутым, ограниченным в пространстве 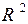 ? Найти его замыкание, внутренность и границу, проиллюстрировать ответ на чертеже (таблица 2.2.1).
? Найти его замыкание, внутренность и границу, проиллюстрировать ответ на чертеже (таблица 2.2.1).
Таблица 2.2.1
2.2.2. Является ли данное множество М открытым, замкнутым, ограниченным в пространстве  ? Найти его замыкание, внутренние и граничные точки (таблица 2.2.2).
? Найти его замыкание, внутренние и граничные точки (таблица 2.2.2).
Таблица 2.2.2
2.2.3. Для данного множества А выяснить, является ли множество  открытым, замкнутым, ограниченным в
открытым, замкнутым, ограниченным в  (таблица 2.2.3).
(таблица 2.2.3).
Таблица 2.2.3

 - метрическое пространство.
- метрическое пространство. .
. 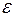 - окрестностью точки а называется открытый шар с центором в точке а радиуса
- окрестностью точки а называется открытый шар с центором в точке а радиуса 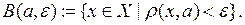
 . Точка а называется внутренней точкой множества А, если она принадлежит А вместе с некоторой своей
. Точка а называется внутренней точкой множества А, если она принадлежит А вместе с некоторой своей  и называется внутренностью множества А.
и называется внутренностью множества А.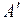 открыто.
открыто.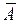 (или
(или  ).
). ;
; для любого
для любого  ;
; для некоторой последовательности
для некоторой последовательности 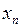 точек множества А.
точек множества А. удовлетворяет условию 2) (или, что равносильно, 3)) предыдущей теоремы, то она называется точкой прикосновения множества А.
удовлетворяет условию 2) (или, что равносильно, 3)) предыдущей теоремы, то она называется точкой прикосновения множества А. .
.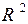 ? Найти его замыкание, внутренность и границу, проиллюстрировать ответ на чертеже (таблица 2.2.1).
? Найти его замыкание, внутренность и границу, проиллюстрировать ответ на чертеже (таблица 2.2.1).




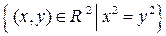
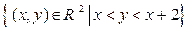


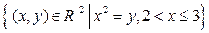
 ? Найти его замыкание, внутренние и граничные точки (таблица 2.2.2).
? Найти его замыкание, внутренние и граничные точки (таблица 2.2.2).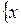






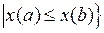
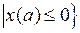


 открытым, замкнутым, ограниченным в
открытым, замкнутым, ограниченным в  (таблица 2.2.3).
(таблица 2.2.3).













