Компактные множества в метрических пространствах
Определение. Подмножество К метрического пространства Х называется компактным (компактом), если из любого его покрытия открытыми множествами можно выбрать конечное покрытие. Определение. Подмножество метрического пространства Х называется предкомпактным (в другой терминологии относительно компактным), если оно содержится в компактном подмножестве пространства Х (это равносильно тому, что его замыкание компактно). Теорема. Подмножество компактно в Х тогда и только тогда, когда оно предкомпактно и замкнуто. Теорема (свойство Больцано-Вейерштрасса). Подмножество К метрического пространства Х компактно тогда и только тогда, когда из любой последовательности его точек можно выбрать подпоследовательность, сходящуюся к точке из К. Теорема. Подмножество К метрического пространства Определение. Подмножество К метрического пространства C [ a, b ] называется равномерно ограниченным, если существует такая константа С, что Определение. Подмножество К метрического пространства C [ a, b ] называется равностепенно непрерывным, если
Теорема Арцела-Асколи. Подмножество К пространства C [ a, b ] предкомпактно тогда и только тогда, когда оно равномерно ограничено и равностепенно непрерывно. Теорема. Подмножество К пространства 1) 2)
2.5.1. Является ли данное множество М а) компактым, б) пред-компактным в пространстве Таблица 2.5.1
2.5.2. Выяснить, является ли множество М предкомпактным, компактным в
Таблица 2.5.2
2.5.3. Определить, является ли данное множество М предком-пактным в пространстве
Таблица 2.5.3
|

 предкомпактно (компактно) тогда и только тогда, когда оно ограничено (соответственно ограничено и замкнуто).
предкомпактно (компактно) тогда и только тогда, когда оно ограничено (соответственно ограничено и замкнуто). .
. .
. предкомпактно тогда и только тогда, когда выполняются следующие два условия:
предкомпактно тогда и только тогда, когда выполняются следующие два условия: ;
; .
. (таблица 2.5.1)?
(таблица 2.5.1)?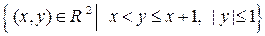



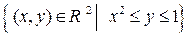





 (таблица 2.5.2).
(таблица 2.5.2).
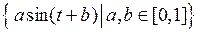








 (таблица 2.5.3).
(таблица 2.5.3). 













