Полнота метрических пространств
Определение. Последовательность
Каждая сходящаяся последовательность фундаментальна, но обратное, вообще говоря, неверно. Определение. Метрическое пространство Важным примером полного метрического пространства служит числовая прямая Теорема. 1) Замкнутое подмножество полного пространства полно. 2) Полное подмножество метрического пространства замкнуто. 2.3.1. Выяснить, является ли последовательность Таблица 2.3.1
Окончание таблицы 2.3.1
(К – канторовское множество).
2.3.2. Выяснить, является ли заданное метрическое пространство
Вариант 1. Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6 Вариант 7 Вариант 8. Вариант 9 Вариант 10 2.3.3. Выяснить, является ли заданное метрическое пространство
Вариант 1. Пространство
Вариант 2. Пространство всех дважды дифференцируемых на отрезке Вариант 3. Пространство Вариант 4. Пространство всех непрерывных на отрезке Вариант 5. Пространство
Вариант 6. Вариант 7. Пространство
Вариант 8.
Вариант 9. Пространство с сходящихся последовательностей Вариант 10. Вариант 11. Пространство Вариант 12.
|

 точек метрического пространства
точек метрического пространства  называется фундаментальной, если
называется фундаментальной, если .
. с естественной метрикой (критерий Коши).
с естественной метрикой (критерий Коши). фундамен-тальной в данном пространстве
фундамен-тальной в данном пространстве  ? Найти
? Найти  , если он существует (таблица 2.3.1).
, если он существует (таблица 2.3.1).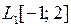



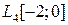

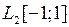



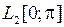




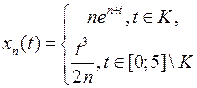




 полным.
полным. ,
, 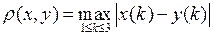 .
. ,
,  .
. .
.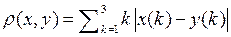 .
. ,
,  .
. .
. ,
,  .
. .
. .
. .
. непрерывно дифференциру-емых на отрезке
непрерывно дифференциру-емых на отрезке  функций с метрикой
функций с метрикой ;
; .
. числовых последова-тельностей
числовых последова-тельностей  , удовлетворяющих условию
, удовлетворяющих условию  , с метрикой
, с метрикой  ;
; .
. всех ограниченных числовых после-довательностей
всех ограниченных числовых после-довательностей  ;
; с метрикой
с метрикой  .
. сходящихся к нулю последова-тельностей
сходящихся к нулю последова-тельностей  с метрикой
с метрикой .
.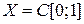 с метрикой
с метрикой  .
. ограниченных и непрерывных на интервале
ограниченных и непрерывных на интервале  функций с метрикой
функций с метрикой  ;
; с метрикой
с метрикой 


