1. Выяснить, являются ли данные множества предкомпактными, компактными в  .
.
Пример 1. а)  ;
;
б)  .
.
Решение. а) Проверим для множества М условия теоремы Арцела-Асколи. Рассмотрим функцию  . Пусть
. Пусть  . Функция
. Функция  непрерывна на
непрерывна на  и
и  . Множество
. Множество  является компактом. По теореме Вейерштрасса функция
является компактом. По теореме Вейерштрасса функция  ограничена на
ограничена на  , т.е.
, т.е.



 .
.
Значит, М равномерно ограничено (впрочем, легко проверить и непосредственно, что при наших условиях  ).
).
Проверим равностепенную непрерывность множества М. Функция  равномерно непрерывна на множестве
равномерно непрерывна на множестве  по теореме Кантора. Если обозначить через
по теореме Кантора. Если обозначить через  произвольную точку из К, то равномерная непрерывность
произвольную точку из К, то равномерная непрерывность  означает, что
означает, что 
 , что
, что  , таких, что
, таких, что  , и
, и  , таких, что
, таких, что  (ρ обозначает евклидову метрику в К), справедливо неравенство
(ρ обозначает евклидову метрику в К), справедливо неравенство
 .
.
Отсюда следует равностепенная непрерывность множества М (см. определение). Значит, по теореме Арцела-Асколи М предкомпактно.
Для доказательства компактности множества М теперь достаточно проверить его замкнутость в  . Но это тоже следует из непрерывности функции
. Но это тоже следует из непрерывности функции  . В самом деле, если х −предельная точка множества М, то найдется последовательность
. В самом деле, если х −предельная точка множества М, то найдется последовательность 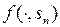 функций из М, сходящаяся к х в
функций из М, сходящаяся к х в  . По теореме Больцано-Вейерштрасса из последовательности
. По теореме Больцано-Вейерштрасса из последовательности  точек множества К можно выбрать подпос-ледовательность, которую мы тоже обозначим
точек множества К можно выбрать подпос-ледовательность, которую мы тоже обозначим  , сходящуюся к точке
, сходящуюся к точке 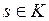 . Тогда поточечно
. Тогда поточечно  , а потому в силу единственности предела
, а потому в силу единственности предела  . Итак, М – компакт.
. Итак, М – компакт.
б) Так как М 1  М, то множество М 1 предкомпактно в силу а). Но М 1 не является компактом, так как не замкнуто в
М, то множество М 1 предкомпактно в силу а). Но М 1 не является компактом, так как не замкнуто в  . Действительно, функции
. Действительно, функции  принадлежат
принадлежат  , но предел этой последовательности
, но предел этой последовательности  не принадлежит множеству М 1.
не принадлежит множеству М 1.
Пример 2.  .
.
Решение. 1 способ. Это множество является равномерно ограниченным, но не является равностепенно непрерывным. Действительно, возьмем  . Тогда
. Тогда 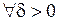 найдется такое натуральное n, что точки
найдется такое натуральное n, что точки  и
и  удовлетворяют неравенству
удовлетворяют неравенству  , но в то же время
, но в то же время  . Значит, по теореме Арцела-Асколи М не является предкомпактным, а потому и компактным множеством.
. Значит, по теореме Арцела-Асколи М не является предкомпактным, а потому и компактным множеством.
2 способ. Множество М не является предкомпактным, так как из него нельзя извлечь подпоследовательность, сходящуюся в  (а потому его замыкание не обладает свойством Больцано-Вейерштрасса). Действительно, все подпоследовательности множества М сходятся к разрывной функции (какой?).
(а потому его замыкание не обладает свойством Больцано-Вейерштрасса). Действительно, все подпоследовательности множества М сходятся к разрывной функции (какой?).
Пример 3.  .
.
Решение. Множество М равномерно ограничено, так как


 .
.
Множество М равностепенно непрерывно, так как 
 и
и  , таких, что
, таких, что  , имеем
, имеем
 .
.
Значит, по теореме Арцела-Асколи М предкомпактно.
Покажем, что М содержит все свои точки прикосновения. Пусть х есть точка прикосновения множества М. Тогда найдутся такие числа  , что
, что  равномерно на
равномерно на  . В силу периодичности синуса можно считать, что
. В силу периодичности синуса можно считать, что  . При этом промежуток
. При этом промежуток 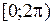 удобно отождествлять с факторгруппой
удобно отождествлять с факторгруппой  , то есть с единичной окружностью, наделенной естественной топологией, в которой она компактна. (Отличие здесь в том, что если последовательность
, то есть с единичной окружностью, наделенной естественной топологией, в которой она компактна. (Отличие здесь в том, что если последовательность  в
в  сходится к
сходится к  , то в этой топологии предел считается равным 0). Заметим, что в этой топологии существует
, то в этой топологии предел считается равным 0). Заметим, что в этой топологии существует  . Действительно, если допустить противное, то найдутся две подпоследовательности
. Действительно, если допустить противное, то найдутся две подпоследовательности  и
и  последовательности
последовательности  , имеющие различные пределы
, имеющие различные пределы  и
и  соответственно. Но тогда
соответственно. Но тогда  при всех t, откуда
при всех t, откуда  . Противоречие. Следовательно,
. Противоречие. Следовательно,  . Значит, М – замкнутое множество, откуда следует, что М – компакт.
. Значит, М – замкнутое множество, откуда следует, что М – компакт.
Пример 4.  .
.
Решение. Данное множество не является равностепенно непрерывным. Действительно, возьмем  . Тогда
. Тогда 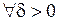 найдется такое натуральное n, что точки
найдется такое натуральное n, что точки  и
и  удовлетворяют неравенству
удовлетворяют неравенству  , но в то же время выполняется неравенство
, но в то же время выполняется неравенство  . Значит, по теореме Арцела-Асколи М не является предкомпактным, а потому и компактным множеством.
. Значит, по теореме Арцела-Асколи М не является предкомпактным, а потому и компактным множеством.
2. Является ли множество М предкомпактным в  ?
?
Пример 1. 
 .
.
Решение. Проверим критерий предкомпактности в  .
.
1) Множество М удовлетворяет первому условию, поскольку, как легко проверить, 
 , а потому
, а потому

 .
.
2) Так как ряд  сходится, то его остаток стремится к нулю, то есть
сходится, то его остаток стремится к нулю, то есть

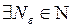
 .
.
Поэтому


 .
.
Значит, множество М предкомпактно.

 .
. ;
; .
. . Пусть
. Пусть  . Функция
. Функция  непрерывна на
непрерывна на  и
и  . Множество
. Множество 


 .
. ).
). произвольную точку из К, то равномерная непрерывность
произвольную точку из К, то равномерная непрерывность 
 , что
, что  , таких, что
, таких, что  , и
, и  , таких, что
, таких, что  (ρ обозначает евклидову метрику в К), справедливо неравенство
(ρ обозначает евклидову метрику в К), справедливо неравенство .
.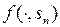 функций из М, сходящаяся к х в
функций из М, сходящаяся к х в  точек множества К можно выбрать подпос-ледовательность, которую мы тоже обозначим
точек множества К можно выбрать подпос-ледовательность, которую мы тоже обозначим 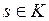 . Тогда поточечно
. Тогда поточечно  , а потому в силу единственности предела
, а потому в силу единственности предела  . Итак, М – компакт.
. Итак, М – компакт. М, то множество М 1 предкомпактно в силу а). Но М 1 не является компактом, так как не замкнуто в
М, то множество М 1 предкомпактно в силу а). Но М 1 не является компактом, так как не замкнуто в  принадлежат
принадлежат  , но предел этой последовательности
, но предел этой последовательности  не принадлежит множеству М 1.
не принадлежит множеству М 1. .
. . Тогда
. Тогда 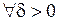 найдется такое натуральное n, что точки
найдется такое натуральное n, что точки  и
и  удовлетворяют неравенству
удовлетворяют неравенству  , но в то же время
, но в то же время  . Значит, по теореме Арцела-Асколи М не является предкомпактным, а потому и компактным множеством.
. Значит, по теореме Арцела-Асколи М не является предкомпактным, а потому и компактным множеством. .
.

 .
. , имеем
, имеем .
. , что
, что  равномерно на
равномерно на  . В силу периодичности синуса можно считать, что
. В силу периодичности синуса можно считать, что  . При этом промежуток
. При этом промежуток 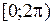 удобно отождествлять с факторгруппой
удобно отождествлять с факторгруппой  , то есть с единичной окружностью, наделенной естественной топологией, в которой она компактна. (Отличие здесь в том, что если последовательность
, то есть с единичной окружностью, наделенной естественной топологией, в которой она компактна. (Отличие здесь в том, что если последовательность  сходится к
сходится к  , то в этой топологии предел считается равным 0). Заметим, что в этой топологии существует
, то в этой топологии предел считается равным 0). Заметим, что в этой топологии существует  . Действительно, если допустить противное, то найдутся две подпоследовательности
. Действительно, если допустить противное, то найдутся две подпоследовательности  и
и  последовательности
последовательности  и
и  соответственно. Но тогда
соответственно. Но тогда  при всех t, откуда
при всех t, откуда  . Противоречие. Следовательно,
. Противоречие. Следовательно,  . Значит, М – замкнутое множество, откуда следует, что М – компакт.
. Значит, М – замкнутое множество, откуда следует, что М – компакт. .
. . Тогда
. Тогда  и
и  удовлетворяют неравенству
удовлетворяют неравенству  , но в то же время выполняется неравенство
, но в то же время выполняется неравенство  . Значит, по теореме Арцела-Асколи М не является предкомпактным, а потому и компактным множеством.
. Значит, по теореме Арцела-Асколи М не является предкомпактным, а потому и компактным множеством. ?
?
 .
.
 , а потому
, а потому
 .
. сходится, то его остаток стремится к нулю, то есть
сходится, то его остаток стремится к нулю, то есть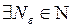
 .
.



