1. Является ли данное множество Т открытым, замкнутым, ограниченным в пространстве 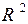 ? Найти его замыкание, внутренность и границу, сделать чертеж.
? Найти его замыкание, внутренность и границу, сделать чертеж.
Пример 1  .
.
Решение. Множество Т есть треугольник, ограниченный прямыми 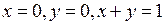 , у которого удалены стороны. Оно открыто. В самом деле, если точка а принадлежит Т, причем положительное число
, у которого удалены стороны. Оно открыто. В самом деле, если точка а принадлежит Т, причем положительное число 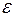 меньше расстояния от а до ближайшей стороны треугольника Т, то
меньше расстояния от а до ближайшей стороны треугольника Т, то 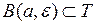 . Следовательно,
. Следовательно, 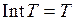 . Далее, присоединяя к множеству Т все его точки прикосновения, получим, что замыкание Т есть треугольник
. Далее, присоединяя к множеству Т все его точки прикосновения, получим, что замыкание Т есть треугольник
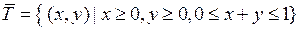
(объясните, почему). Следовательно, Т не замкнуто, и  есть объединение сторон этого треугольника. Наконец, очевидно, что множество Т ограничено. Выполнение чертежа оставляем читателю.
есть объединение сторон этого треугольника. Наконец, очевидно, что множество Т ограничено. Выполнение чертежа оставляем читателю.
2. Является ли данное множество 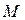 открытым, замкнутым, ограниченным в пространстве
открытым, замкнутым, ограниченным в пространстве 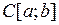 ? Найти его замыкание, внутренние и граничные точки.
? Найти его замыкание, внутренние и граничные точки.
Пример 1. 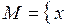
 .
.
Решение. Множество М не является открытым, и более того, ни одна его точка не является внутренней. Действительно, для любой  и для любого шара
и для любого шара  имеем
имеем 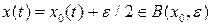 , но
, но 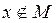 , так как
, так как 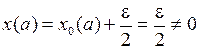 . Следовательно,
. Следовательно, 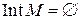 .
.
Множество М является замкнутым, так как оно содержит все свои точки прикосновения. Действительно, пусть 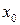 есть точка прикосновения множества М. Тогда
есть точка прикосновения множества М. Тогда  в
в 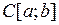 для некоторой последовательности
для некоторой последовательности 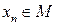 . Но равенства
. Но равенства 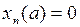 влекут
влекут 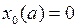 (почему?). А это значит, что
(почему?). А это значит, что 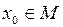 .
.
Граница множества 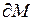 совпадает с самим множеством М, что теперь сразу следует из формулы
совпадает с самим множеством М, что теперь сразу следует из формулы  .
.
Множество М не является ограниченным, так как, например, после-довательность  принадлежит М, но
принадлежит М, но
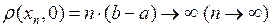 .
.
Пример 2. 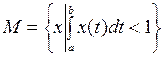 .
.
Решение. Покажем, что М является открытым. Возьмём произвольную точку  . Так как
. Так как  , то найдется такое
, то найдется такое  , что
, что 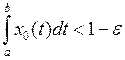 . Покажем, что
. Покажем, что  . В самом деле, для любого
. В самом деле, для любого  справедливо неравенство
справедливо неравенство
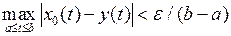 .
.
Поэтому
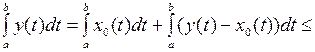
 .
.
Значит, 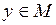 .
.
Так как М открыто, то 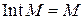 .
.
Множество М не является замкнутым, так как содержит не все свои точки прикосновения. Действительно, возьмём последовательность 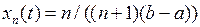 точек из М. Тогда
точек из М. Тогда  , но
, но  , т.е. постоянная функция
, т.е. постоянная функция 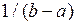 не принадлежит М.
не принадлежит М.
Замечание. Так как любые две точки  можно связать непрерывным путем
можно связать непрерывным путем 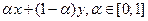 , лежащим в
, лежащим в  , то пространство
, то пространство  (и вообще любое нормированное пространство) всегда связно,и поэтому в нем нет открытых и одновременно замкнутых собственных подмножеств.
(и вообще любое нормированное пространство) всегда связно,и поэтому в нем нет открытых и одновременно замкнутых собственных подмножеств. 
Теперь покажем, что 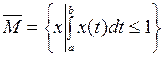 . Действительно, если
. Действительно, если  принадлежит
принадлежит  , то найдется последовательность
, то найдется последовательность 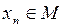 , равномерно сходящаяся к
, равномерно сходящаяся к  на
на 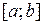 . А тогда
. А тогда
 .
.
Обратно, если 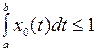 , то последовательность
, то последовательность  принадлежит М и сходится к
принадлежит М и сходится к  равномерно (проверьте!), а потому
равномерно (проверьте!), а потому  принадлежит
принадлежит  .
.
Теперь ясно, что

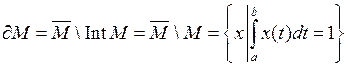 .
.
Наконец, М не является ограниченным, так как, наприммер, последовательность постоянных функций  принадлежит М, но
принадлежит М, но  .
.
Пример 3. 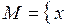
 .
.
Решение. Покажем, что М открыто. Пусть  . Тогда
. Тогда  , а потому
, а потому  для некоторого
для некоторого  . Для любого
. Для любого 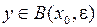 имеем
имеем  , и следовательно,
, и следовательно,
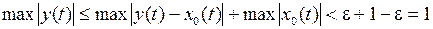 ,
,
т. е.  . Таким образом, точка x 0 – внутренняя для М.
. Таким образом, точка x 0 – внутренняя для М.
Покажем, что

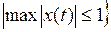 .
.
Действительно, если  принадлежит
принадлежит  , то найдется последовательность
, то найдется последовательность 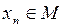 , равномерно сходящаяся к
, равномерно сходящаяся к  на
на 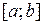 . А тогда
. А тогда  , т. е.
, т. е.  принадлежит М.
принадлежит М.
Обратно, если 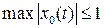 , то последовательность
, то последовательность  принадлежит М и сходится к
принадлежит М и сходится к  равномерно на
равномерно на 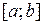 (проверьте), а потому
(проверьте), а потому  принадлежит
принадлежит  .
.
Теперь ясно, что
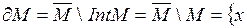
 .
.
Очевидно, что данное множество ограничено.
3. Для данного множества А выяснить, является ли множество  открытым, замкнутым, ограниченным в
открытым, замкнутым, ограниченным в 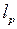 .
.
Пример 1. 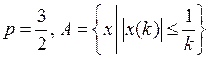 .
.
Решение. Множество 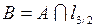 замкнуто, так как содержит в себе все свои точки прикосновения. Действительно, если
замкнуто, так как содержит в себе все свои точки прикосновения. Действительно, если  есть точка прикосновения множества В, то найдется такая последовательность
есть точка прикосновения множества В, то найдется такая последовательность  что
что 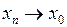 в
в  . Отсюда следует, что при всех
. Отсюда следует, что при всех  имеем
имеем  (почему?). Но так как
(почему?). Но так как 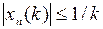 , то и
, то и  . Значит,
. Значит, 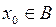 .
.
Так как 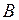 замкнуто, то оно не является открытым, поскольку пространство
замкнуто, то оно не является открытым, поскольку пространство 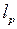 связно (см. замечание к примеру 2 в задаче 1). Но легко дать и прямое доказательство. Действительно, точка
связно (см. замечание к примеру 2 в задаче 1). Но легко дать и прямое доказательство. Действительно, точка 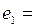
 принадлежит
принадлежит 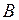 , но для любого
, но для любого 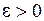 точка
точка  не принадлежит В, хотя и лежит в
не принадлежит В, хотя и лежит в 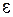 -окрестности точки
-окрестности точки  . Следовательно, точка
. Следовательно, точка  не является внутренней для В.
не является внутренней для В.
Наконец,  ограничено, так как
ограничено, так как  при всех
при всех 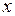 из множества В справедливо неравенство
из множества В справедливо неравенство
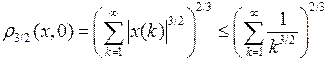 .
.
Пример 2. 
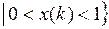 .
.
Решение. Множество  не является открытым. Для доказательства покажем, что точка
не является открытым. Для доказательства покажем, что точка  не является для него внутренней. Возьмём
не является для него внутренней. Возьмём  и найдём такое натуральное N, что
и найдём такое натуральное N, что  . Тогда
. Тогда
 ,
,
но  , поскольку
, поскольку 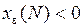 .
.
Множество  не замкнуто. Действительно, рассмотрим последовательность
не замкнуто. Действительно, рассмотрим последовательность 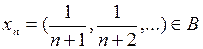 . Тогда
. Тогда  сходится к точке
сходится к точке 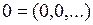 , так как
, так как  при
при  , но
, но  .
.
Множество  ограничено, так как
ограничено, так как  при всех
при всех 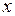 из В.
из В.
Пример 3. 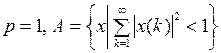 .
.
Решение. Покажем, что множество  открыто.
открыто.
Для любого элемента 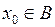 найдется такое
найдется такое  , что
, что
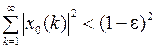 .
.
Если 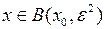 (шар рассматривается, конечно, в
(шар рассматривается, конечно, в 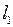 ), то
), то
 .
.
Тогда и
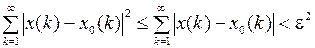 .
.
Теперь в силу неравенства Минковского имеем
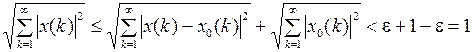 .
.
Значит, 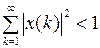 , т. е.
, т. е.  . Итак,
. Итак,  .
.
Так как  открыто, то
открыто, то  не замкнуто по замечанию из решения примера 2 к задаче 1. Дадим прямое доказательство этого факта. Точки
не замкнуто по замечанию из решения примера 2 к задаче 1. Дадим прямое доказательство этого факта. Точки 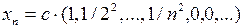 , где
, где  , очевидно, принадлежат
, очевидно, принадлежат  . Но в то же время
. Но в то же время  сходится в
сходится в 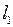 к
к  .
.
Покажем, что  не ограничено. Рассмотрим последовательность
не ограничено. Рассмотрим последовательность
 .
.
Имеем  , так как
, так как
 ,
,
но в то же время
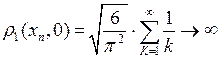 при
при  .
.
Пример 4. 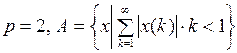 .
.
Решение. Покажем, что 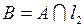 не является открытым. Возьмём
не является открытым. Возьмём 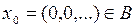 и
и  . Найдётся такое натуральное
. Найдётся такое натуральное 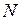 , что
, что 
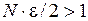 . Тогда
. Тогда 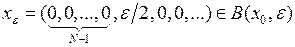 , но
, но  .
.
Множество  не является и замкнутым. Для доказательства рассмотрим последовательность
не является и замкнутым. Для доказательства рассмотрим последовательность
 .
.
Она сходится к точке
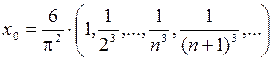 ,
,
которая не принадлежит  , так как
, так как
 .
.
Множество  ограничено, поскольку неравенство
ограничено, поскольку неравенство 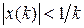 влечет оценку
влечет оценку
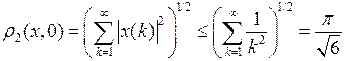 .
.

 ? Найти его замыкание, внутренность и границу, сделать чертеж.
? Найти его замыкание, внутренность и границу, сделать чертеж. .
.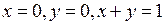 , у которого удалены стороны. Оно открыто. В самом деле, если точка а принадлежит Т, причем положительное число
, у которого удалены стороны. Оно открыто. В самом деле, если точка а принадлежит Т, причем положительное число 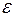 меньше расстояния от а до ближайшей стороны треугольника Т, то
меньше расстояния от а до ближайшей стороны треугольника Т, то 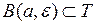 . Следовательно,
. Следовательно, 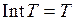 . Далее, присоединяя к множеству Т все его точки прикосновения, получим, что замыкание Т есть треугольник
. Далее, присоединяя к множеству Т все его точки прикосновения, получим, что замыкание Т есть треугольник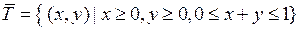
 есть объединение сторон этого треугольника. Наконец, очевидно, что множество Т ограничено. Выполнение чертежа оставляем читателю.
есть объединение сторон этого треугольника. Наконец, очевидно, что множество Т ограничено. Выполнение чертежа оставляем читателю.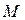 открытым, замкнутым, ограниченным в пространстве
открытым, замкнутым, ограниченным в пространстве 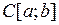 ? Найти его замыкание, внутренние и граничные точки.
? Найти его замыкание, внутренние и граничные точки.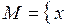
 .
. и для любого шара
и для любого шара  имеем
имеем 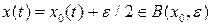 , но
, но 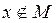 , так как
, так как 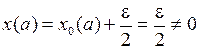 . Следовательно,
. Следовательно, 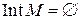 .
.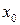 есть точка прикосновения множества М. Тогда
есть точка прикосновения множества М. Тогда  в
в 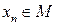 . Но равенства
. Но равенства 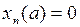 влекут
влекут 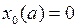 (почему?). А это значит, что
(почему?). А это значит, что 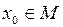 .
.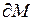 совпадает с самим множеством М, что теперь сразу следует из формулы
совпадает с самим множеством М, что теперь сразу следует из формулы  .
. принадлежит М, но
принадлежит М, но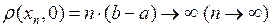 .
.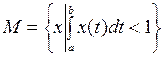 .
. . Так как
. Так как  , то найдется такое
, то найдется такое  , что
, что 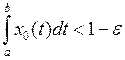 . Покажем, что
. Покажем, что  . В самом деле, для любого
. В самом деле, для любого  справедливо неравенство
справедливо неравенство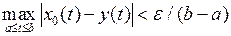 .
.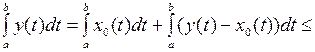
 .
.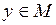 .
.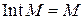 .
.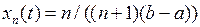 точек из М. Тогда
точек из М. Тогда  , но
, но  , т.е. постоянная функция
, т.е. постоянная функция 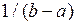 не принадлежит М.
не принадлежит М. можно связать непрерывным путем
можно связать непрерывным путем 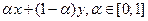 , лежащим в
, лежащим в  , то пространство
, то пространство 
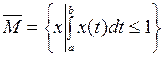 . Действительно, если
. Действительно, если  принадлежит
принадлежит  , то найдется последовательность
, то найдется последовательность 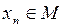 , равномерно сходящаяся к
, равномерно сходящаяся к 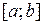 . А тогда
. А тогда .
.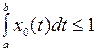 , то последовательность
, то последовательность  принадлежит М и сходится к
принадлежит М и сходится к 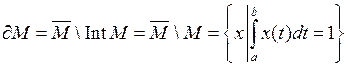 .
. принадлежит М, но
принадлежит М, но  .
. .
. , а потому
, а потому  для некоторого
для некоторого  . Для любого
. Для любого 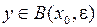 имеем
имеем  , и следовательно,
, и следовательно,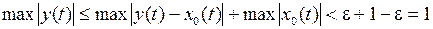 ,
, . Таким образом, точка x 0 – внутренняя для М.
. Таким образом, точка x 0 – внутренняя для М.
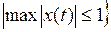 .
. , т. е.
, т. е. 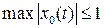 , то последовательность
, то последовательность 
 .
. открытым, замкнутым, ограниченным в
открытым, замкнутым, ограниченным в  .
.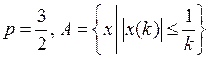 .
.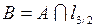 замкнуто, так как содержит в себе все свои точки прикосновения. Действительно, если
замкнуто, так как содержит в себе все свои точки прикосновения. Действительно, если  что
что 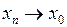 в
в  . Отсюда следует, что при всех
. Отсюда следует, что при всех  имеем
имеем  (почему?). Но так как
(почему?). Но так как 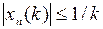 , то и
, то и  . Значит,
. Значит, 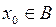 .
.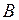 замкнуто, то оно не является открытым, поскольку пространство
замкнуто, то оно не является открытым, поскольку пространство 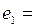
 принадлежит
принадлежит 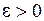 точка
точка  не принадлежит В, хотя и лежит в
не принадлежит В, хотя и лежит в 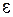 -окрестности точки
-окрестности точки  . Следовательно, точка
. Следовательно, точка  ограничено, так как
ограничено, так как 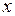 из множества В справедливо неравенство
из множества В справедливо неравенство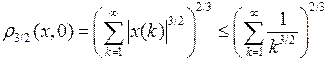 .
.
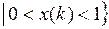 .
. не является открытым. Для доказательства покажем, что точка
не является открытым. Для доказательства покажем, что точка  не является для него внутренней. Возьмём
не является для него внутренней. Возьмём  . Тогда
. Тогда ,
, , поскольку
, поскольку 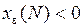 .
.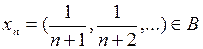 . Тогда
. Тогда  сходится к точке
сходится к точке 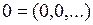 , так как
, так как  при
при  , но
, но  .
. при всех
при всех 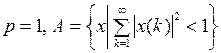 .
. открыто.
открыто.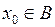 найдется такое
найдется такое  , что
, что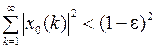 .
.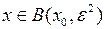 (шар рассматривается, конечно, в
(шар рассматривается, конечно, в 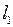 ), то
), то .
.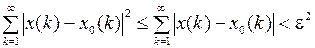 .
.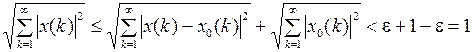 .
.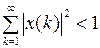 , т. е.
, т. е.  . Итак,
. Итак,  .
.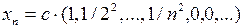 , где
, где  , очевидно, принадлежат
, очевидно, принадлежат  .
. .
. , так как
, так как ,
,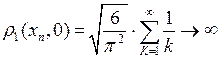 при
при 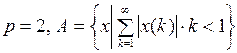 .
.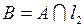 не является открытым. Возьмём
не является открытым. Возьмём 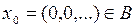 и
и 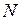 , что
, что 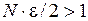 . Тогда
. Тогда 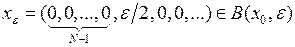 , но
, но  .
. .
.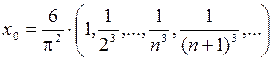 ,
, .
.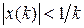 влечет оценку
влечет оценку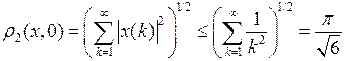 .
.


