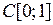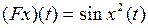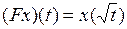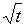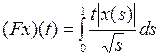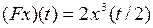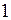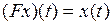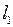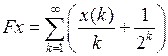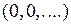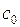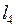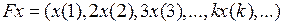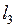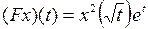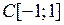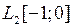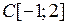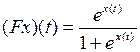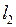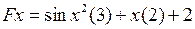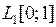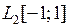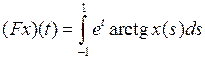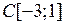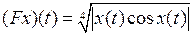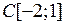Тема 2.4
Непрерывные отображения Далее Определение. Пусть Это равносильно тому, что из того, что Отображение f называется непрерывным, если оно непрерывно в каждойточке множества Х. Определение. Отображение f называется равномерно непрерыв-ным на множестве Х, если для любого Определение. Говорят, что отображение f удовлетворяет условию Липшица, если существует такое число Ясно, что из условия Липшица следует равномерная непрерывность, а из последней – непрерывность отображения f.
2.4.1. Выяснить, является ли заданное отображение Таблица 2.4.1
Окончание таблицы 2.4.1
2.4.2. Является ли заданное отображение а) непрерывным; б) равномерно непрерывным; в) удовлетворяющим условию Липшица (таблица 2.4.2)? Таблица 2.4.2
|
и 
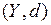– метрические пространства, 
.
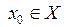. Отображение f называется непре-рывным в точке 
, если для любого 
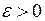существует такое 
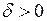, что из неравенства 
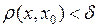следует неравенство 
(непрерывность «на языке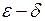 
»).
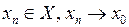, следует, что 
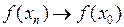при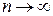 
(непрерывность «на языке последова-тельностей»).
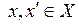из неравенства 
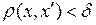следует неравенство 
.
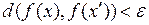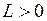, что для любых 
.
на своей естественной области определения непрерывным в точке 
(таблица 2.4.1)?
