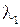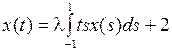Всюду ниже  - метрическое пространство.
- метрическое пространство.
Определение. Отображение  называется сжимающим, если оно удовлетворяет условию Липшица с константой Липшица
называется сжимающим, если оно удовлетворяет условию Липшица с константой Липшица  . Другими словами, существует такое
. Другими словами, существует такое  , что при всех
, что при всех  выполняется неравенство
выполняется неравенство

Определение. Точка  из Х называется неподвижной для отображения
из Х называется неподвижной для отображения  , если
, если  .
.
Теорема (принцип сжимающих отображений). Сжимающее отображение А полного метрического пространства в себя имеет неподвижную точку, причем ровно одну.
При этом неподвижная точка  может быть найдена методом последовательных приближений (итераций), т.е. как предел последовательности, заданной рекуррентным соотношением
может быть найдена методом последовательных приближений (итераций), т.е. как предел последовательности, заданной рекуррентным соотношением  , где
, где  выбирается произвольно.
выбирается произвольно.
Оценка абсолютной погрешности приближенного равенства  дается формулой
дается формулой
 .
.
Теорема. Пусть k(t,s) и g(t) - непрерывные функции ( ). Отображение
). Отображение

в пространстве  является сжимающим, если и только если
является сжимающим, если и только если  , где
, где  . При этом
. При этом  .
.
2.6.1. Является ли отображение F метрического пространства X в себя сжимающим? Найти  , где
, где  . Оценить расстояние от
. Оценить расстояние от  до неподвижной точки в случае, если F является сжимающим (таблица 2.6.1).
до неподвижной точки в случае, если F является сжимающим (таблица 2.6.1).
Таблица 2.6.1
2.6.2. Применим ли принцип сжимающих отображений к заданному интегральному уравнению в пространстве Х при 
 ? При
? При  найти приближенное решение с точностью до 0,01 и сравнить его с точным решением (таблица 2.6.2).
найти приближенное решение с точностью до 0,01 и сравнить его с точным решением (таблица 2.6.2).
Таблица 2.6.2

 - метрическое пространство.
- метрическое пространство. называется сжимающим, если оно удовлетворяет условию Липшица с константой Липшица
называется сжимающим, если оно удовлетворяет условию Липшица с константой Липшица  . Другими словами, существует такое
. Другими словами, существует такое  , что при всех
, что при всех  выполняется неравенство
выполняется неравенство
 из Х называется неподвижной для отображения
из Х называется неподвижной для отображения  .
. может быть найдена методом последовательных приближений (итераций), т.е. как предел последовательности, заданной рекуррентным соотношением
может быть найдена методом последовательных приближений (итераций), т.е. как предел последовательности, заданной рекуррентным соотношением  , где
, где  выбирается произвольно.
выбирается произвольно. дается формулой
дается формулой .
. ). Отображение
). Отображение
 является сжимающим, если и только если
является сжимающим, если и только если  , где
, где  . При этом
. При этом  .
. , где
, где  . Оценить расстояние от
. Оценить расстояние от 


















 ? При
? При  найти приближенное решение с точностью до 0,01 и сравнить его с точным решением (таблица 2.6.2).
найти приближенное решение с точностью до 0,01 и сравнить его с точным решением (таблица 2.6.2).