Координаты центра давления.
Центр давления, как и центр масс для машины, нагрузки которых на опорное основание в процессе выполнения технологических операций меняют свою величину, также меняют свое положение. Поэтому их координаты определяются для нескольких состояний машины, например, для рабочего положения и транспортного. Это особенно актуально для положения центра давления, которое зависит как от сил тяжести, так и других внешних нагрузок на машину (крюковое усилие, сила противодействия разрабатываемой породы на массив и т.п.). В нашем случае центр р давления меняет свое положение при заполнении ковша и его перемещении относительно машины. Для большинства машин подобного типа положение центра давления находят в двух положениях: при действии внешних дополнительных нагрузок и в свободном от них состоянии. Так как координаты центра масс определены при заполненном породой ковше на максимальном его вылете и другие внешние нагрузки на машину не действуют, то в этом положении нет необходимости специально определять координаты центра давления, т.к. в этой ситуации
Для определения координат центра давления в транспортном положении повторим вычисления по уже примененным формулам, начиная с заполнения таблицы 4, в которой исключаем массу породы в ковше. Полученные результаты снабдим меткой «´».
Как и в положении машины с заполненным породой ковшом координаты центра давления совпадают с координатами центра масс
Строим ядро сечения опорной поверхности и наносим точки, соответствующие центрам давления в обоих случаях (Рис.8). Если центр давления расположен в пределах ядра сечения, то общую компоновку машины можно считать удовлетворительной. После определения положения центра давления выбираем тип и размеры шин. В качестве исходного параметра для выбора шин используем максимальную нагрузку на колеса. Для обеспечения требуемой грузоподъемности по максимальной нагрузке на колесо Pzn =34000 Н выбираем шины 37.0-508 (12-20). Основные параметры шин следующие: ширина профиля В = 0,45 м; свободный радиус rc = 0,61 м; статический радиус rcm = 0,56 м; внутреннее давление воздуха рв = 0,42 МПа; максимальная нагрузка Рzn = 37800 Н (3850 кг).
Рис. 8. Положение центра давления в обоих случаях.
Исходя из этих данных и нагрузки на колесо определяем площадь Sк контакта шины с опорной поверхностью предварительно вычислив половину длины пятна контакта. Для вычисления этой величины определяем радиальную деформацию h к.
где Pzп - грузоподъемность шины.
Тогда
Максимальное давление шины на опорное основание
Деформация опорной поверхности (подошвы выработки) под наиболее нагруженным колесом
Эта деформация пренебрежительно мала. Модуль Юнга опорной поверхности принят равным 2х104 МПа [2].
|

 ,
, 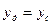 . (40)
. (40)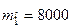 кг
кг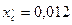 м;
м;  м;
м; 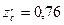 м;
м; H;
H; H;
H;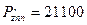 H;
H; 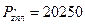 H;
H;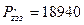 H;
H; 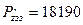 H.
H. м;
м; 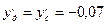 м.
м.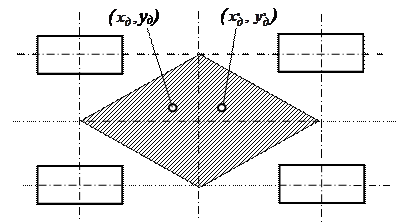
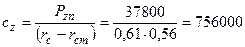
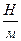 = 760 кН/м,
= 760 кН/м, м.
м.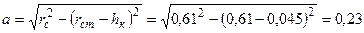 м;
м;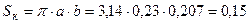 м2.
м2.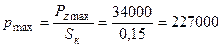 Па = 227 кПа.
Па = 227 кПа.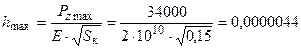 м = 0,0044 мм.
м = 0,0044 мм.


