Давление на опорную поверхность.
При расчете колесных движителей на пневматических колесах важное значение имеет давление в пятне контакта колеса с дорогой. Среднее давление определяют по формуле
где Pz - вертикальная нагрузка на колесо; Sк - площадь контакта колеса с опорным основанием. Нормальная к опорной поверхности нагрузка Pz на каждое колесо (Рис.2) определяется из условий равновесия машины в вертикальной плоскости
Рис. 3. Расчетная схема двухосной машины
. Эти условия записываются в виде
где n - число колес ходового устройства машины; Pzi – нормальная к опорной поверхности нагрузка на i -е колесо. Rz - общая реакция опорной поверхности на машину (равнодействующая всех нормальных реакций колес); xд, yд - координаты центра давления; MOy(Pzi), MOx(Pzi) - моменты внешних сил относительно осей Ox и Oy. Конкретный вид этих уравнений зависит от конструкции ходового устройства, подвески колес, вида рабочего оборудования и ряда других факторов, характер действия которых обычно учитывается в дополнительных уравнениях к системе (3). Работа колесного движителя существенно зависит от распределения нагрузок по колесам, т.е. от положения центра давления. Рассмотрим двухосный колесный движитель горной машины на жестких колесах (рис.3). На машину действует сила тяжести, нагрузки со стороны разрабатываемой породы Р и реакции опорной поверхности на колеса. Под действием этих сил она находится в равновесии. Для нормальной работы ходового устройства необходимо, чтобы все колеса передавали нагрузку на опорную поверхность. Выполнение этого условия обеспечивается тогда, когда центр давления находится в пределах ядра сечения опорной поверхности. Размеры и форма ядра сечения, как и в случае гусеничных машин [1], в основном зависит от типа колес (жесткие, упругие) и подвески. Для определения его формы и размеров определим экстремальные значения давления по формуле
где P z0 - общая нормальная к опорной поверхности нагрузка машины на опорное основание; S 0 - суммарная площадь контакта колес с опорной поверхностью; M x, M y - моменты внешних сил относительно соответствующих осей; W x, W y - моменты сопротивления опорной площади относительно тех же осей. Приравняем теперь к нулю минимальное значение давления, вычислив предварительно величины M x, M y, W x и W y. Для равных по площади контактных площадок двухосной машины
где S к - площадь контакта одного колеса. Моменты сопротивления опорной площади движителя
где I x, I y - моменты инерции опорной площади относительно соответствующих осей; x max, y max - максимальные значения координат контактных площадок. Моменты инерции, учитывая малость контактных площадок колес по сравнению с общими размерами опорной площади ходового устройства, вычисляем по упрощенным формулам
Примем
Учитывая, что
или
где хдм, удм - координаты границ ядра сечения. Как и в случае двухгусеничной машины [1] с жесткой подвеской соотношение (10) указывает на то, что контур ядра сечения колесной двухосной машины на жестких колесах ограничен прямыми линиями. Ядро сечения представляет собой ромб с диагоналями, равными d и a (Рис.3). Максимальные значения границ ядра сечения
Таким же образом определяем размеры ядра сечения трехосного и четырехосного хода (Рис.4,а и рис.4,б). Колесные машины на пневматических шинах и с упругой подвеской колес имеют ядро сечения другой формы и больших размеров. Поэтому допустимое положение центра давления для жестких колесных машин тем более допустимо для машин на пневматических шинах с упругой подвеской колес. Применяя формулу (4) для трехосной и четырехосной машин с жесткими колесами и повторяя последовательность определения размеров ядра сечения двухосной машины, имеем - для трехосной машины
условие равенства нулю минимального значения р
или
откуда
Рис. 4 (а,б). Ядра сечения трехосной (а) и четырехосной (б) машин
- для четырехосной машины
Представляет практический интерес определение размеров ядра сечения колесного хода с шарнирным соединением переднего моста с рамой, задний мост к которой крепится жестко (Рис.5). Так как для колесного хода условие Суммарные реакции на колеса переднего и заднего мостов
где
Rпл, Rзл, Rпп, Rзп, - реакции опорного основания на колеса левого и правого бортов соответственно переднего и заднего мостов.
(16)
Приравняв к нулю эти реакции, убеждаемся, что ядро сечения такого хода – прямоугольник со сторонами d2 и а, т.е. максимально возможные координаты центра давления для такого колесного хода
Рис. 5. К определению размеров ядра сечения двухосного колесного движителя с шарнирным соединением переднего моста и рамы.
Определим размеры пятна контакта колеса, считая, что величины P zi определены. Площадь пятна контакта колеса с опорным основанием зависит от его конструкции и величины нормальной нагрузки P zi. Форма пятна контакта также весьма различна и может меняться от круга до прямоугольника. Чаще всего пятно контакта имеет форму овала и его площадь может быть определена по формуле
где a и b - полуоси элипcа (реально это половины длины и ширины пятна контакта). Для практических расчетов размер b принимается равным половине ширины беговой дорожки шины, а размер а вычисляется по формуле
где rc - свободный радиус колеса; hк - деформация шины. Деформацию hк шины можно вычислить, используя выражение
где сz - радиальная жесткость шины. Значения радиальной жесткости шин зависит от типа и размеров шины, а также внутреннего давления воздуха. При номинальном давлении радиальная жесткость может быть найдена из справочных данных каталогов заводов-изготовителей шин, где обычно указываются номинальная грузоподъемность, давление воздуха в шине, свободный и статический радиусы. В этом случае радиальная жесткость
где rc - свободный радиус шины; rcт - статический радиус при нормальной нагрузке; Рzn - номинальная грузоподъемность. Определив давление колес на опорную поверхность
|

 , (2)
, (2)
 ,
, , (3)
, (3) ,
, , (4)
, (4) , (5)
, (5) ,
,  , (6)
, (6)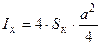 ;
;  , (7)
, (7) ,
,  . Тогда
. Тогда ;
;  , (8)
, (8) ,
,  и подставив эти значения, а также значения W x и W y в (4) и принимая во внимание то, что на границе ядра сечения
и подставив эти значения, а также значения W x и W y в (4) и принимая во внимание то, что на границе ядра сечения  , имеем
, имеем , (9)
, (9) , (10)
, (10)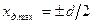 ,
,  . (11)
. (11) ;
;  ;
;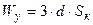
 ,
, ,
, ;
;  . (12)
. (12)
 ;
; ;
; ;
; .
. ,
,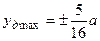 . (13)
. (13) ;
;  , (14)
, (14) - общая реакция грунта на передний мост;
- общая реакция грунта на передний мост; - то же на задний мост;
- то же на задний мост; ; (15)
; (15) ;
; .
. ;
;  . (17)
. (17)
 , (18)
, (18) , (19)
, (19)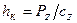 , (20)
, (20) , (21)
, (21)


