Движение колеса по деформируемому основанию.
Колесные машины, используемые при проведении горных работ, очень часто перемещаются вне дорожной сети, т.е. работают на деформируемых опорных основаниях. Сопротивление движению в таких случаях очень зависит от деформаций опорного основания. Более того, движение может быть даже невозможным (посадка машины на раму или днище). При работе колеса в таких условиях коэффициент сопротивления движению может быть рассчитан по формуле
где h - деформация грунта под колесом; D=2·rc - диаметр колеса в свободном состоянии; φ = 0,6÷0,9 - поправочный коэффициент, меньшие значения которого соответствуют деформируемым колесам и наоборот. Деформация грунта под колесами зависит от его физико-механических свойств и упругих свойств шины. Для ее определения воспользуемся формулой для определения деформации основания под круглым штампом радиуса R [1]
где ν – коэффициент Пуассона материала опорного основания; E - модуль упругости опорного основания. Преобразуем эту формулу следующим образом
где
Множитель Для более ассиметричных площадок значения множителя меньше. Однако учитывая реальные значения коэффициента Пуассона (ν ≈ 0,3) для практических проектных расчетов рекомендуется формула
Формулы (27-29) являются модернизацией формулы проф. Опейко Ф.А. [1], предложенной для определения деформации опорного основания под ходовыми устройствами при действии закона Гука. При определении деформации h опорного основания по формуле (29) необходимо учитывать, что площадь Sк пятна контакта зависит от деформации колеса и формы пятна контакта. Например, для наиболее распространенных форм пятна контакта – овала (эллипса) Sк = π · а·b. В свою очередь половину длины контакта (5) с учетом того, что в реальных условиях
В этом случае деформация опорного основания под деформируемым колесом
Возведя (20) в четвертую степень и учитывая, что
откуда
При использовании формул (27-32) следует учитывать, что они являются приближенными. Более подробно движение колеса описывается в специальной литературе по колесным машинам. Однако в большинстве случаев приведенные зависимости дают результаты достаточно точные для практических расчетов.
|

 , (26)
, (26) , (27)
, (27) ; (28)
; (28) - площадь контакта;
- площадь контакта; - среднее давление в контакте.
- среднее давление в контакте. в этой формуле относится к контактной площадке в форме круга.
в этой формуле относится к контактной площадке в форме круга.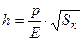 . (29)
. (29) , можно вычислить по приближенной формуле
, можно вычислить по приближенной формуле . (30)
. (30)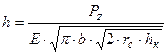 . (31)
. (31)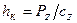 , имеем
, имеем ,
, . (32)
. (32)


