Завдання 7.11
Необхідно: – за даними таблиці 7.9 обчислити параметри лінійного рівняння регресії, надати їм економічну інтерпретацію; – за допомогою коефіцієнта детермінації визначити тісноту зв’язку між урожайністю кукурудзи та строком її збирання. – перевірити істотність зв’язку між зазначеними ознаками з імовірністю 0,95.
Дані для виконання: Таблиця 7.9. Залежність урожайності кукурудзи від строку збирання урожаю обстежено 10 господарств, які належать до однієї природно-кліматичної зони
Розв’язок. Результативною ознакою y є урожайність кукурудзи, а факторною x – строк збирання урожаю. Для оцінки параметрів лінійного рівняння регресії складають систему нормальних рівнянь, що має вигляд
Розрахункові суми для складання систем нормальних рівнянь наведено в таблиці 7.10. Отже, Таблиця 7.10. Розрахунок сум для складання систем нормальних рівнянь
392 = 10 b 0 + 237 b 1; 8731 = 237 b 0 + 5895 b 1. Після розв’язку цієї системи будь-яким способом одержимо Y = 86,87 – 2,01 x. При збільшенні строку збирання урожаю кукурудзи на один день її урожайність знижується в середньому на 2,01 ц/га. На підставі рівняння регресії обчислюють теоретичні значення Y для всіх елементів сукупності. Наприклад, для першого господарства Y 1 = 86,87 – 2,01х27 = 32,6 ц/га. Теоретичні значення Y використовують для обчислення коефіцієнту детермінації
де Отже, Таким чином, 85,3% варіації урожайності кукурудзи лінійно пов’язані зі строком збирання урожаю. Перевірку істотності зв’язку здійснюють за допомогою F-критерію, або k 1 = m – 1 = 2 – 1 = 1; k 2 = n – m = 10 – 2 = 8, де m – число параметрів рівняння регресії для лінійного рівняння (m = 2), а n – кількість елементів сукупності (n = 10). Критичне значення
|


 ,
, – факторна,
– факторна,  – загальна дисперсія.
– загальна дисперсія.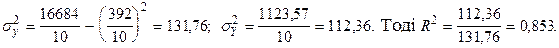
 для ступенів вільнoсті:
для ступенів вільнoсті: для імовірності 0,95 згідно з додатком становить
для імовірності 0,95 згідно з додатком становить  (1,8) = 0,399. Фактичне значення
(1,8) = 0,399. Фактичне значення 


