Необхідно:
– за даними таблиці 7.12 обчислити коефіцієнт співзалежності; з імовірністю 0,95 перевірити істотність зв’язку між ознаками.
Дані для виконання:
Таблиця7.12. Дані комбінаційного розподілу подружніх пар за віком, років
| Вік дружини
| Вік чоловіка
| Разом
|
| 15 – 29
| 30 – 44
| 45 і більше
|
| 15 – 29
|
|
|
|
|
| 30 – 44
|
|
|
|
|
| 45 і більше
| -
|
|
|
|
| Разом
|
|
|
|
|
Розв’язок. Оскільки число груп за обома ознаками однакове, використовуємо формулу коефіцієнта співзалежності Чупрова
 ,
,
де c  =
= 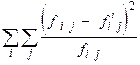 – сума стандартизованих відхилень фактичних частот розподілу від теоретичних; m 1 та m 2 – кількість груп за першою і другою ознаками; n – кількість елементів сукупності.
– сума стандартизованих відхилень фактичних частот розподілу від теоретичних; m 1 та m 2 – кількість груп за першою і другою ознаками; n – кількість елементів сукупності.
Розрахунок c  подано в таблиці 7.13. Теоретичні частоти обчислюють на основі підсумкових частот
подано в таблиці 7.13. Теоретичні частоти обчислюють на основі підсумкових частот  .
.
Наприклад,  і т. д.
і т. д.
Таблиця7.13. Розрахункова таблиця
|
Група i j
|
f i j
|
f ‘ i j
|
f i j – f ‘ i j
|
(f i j – f ‘ i j)
|
(f i j – f ‘ i j) / f ‘ i j
|
|
|
|
|
|
| 28,0
|
|
|
|
| -6
|
| 3,3
|
|
|
|
| -8
|
| 7,1
|
|
|
|
| -7
|
| 4,4
|
|
|
|
|
|
| 13,1
|
|
|
|
| -5
|
| 8,0
|
|
|
|
| -7
|
| 7,0
|
|
|
|
| -7
|
| 4,1
|
|
|
|
|
|
| 19,6
|
| Разом
|
|
|
| -
| 96,3
|
Коефіцієнт співзалежності становить 0,49, тобто
 .
.
Перевірку істотності зв’язку здійснюють за допомогою критерію c  з числом ступенів вільності K = (m 1 – 1) (m 2 – 1) = 2 x 2 = 4.
з числом ступенів вільності K = (m 1 – 1) (m 2 – 1) = 2 x 2 = 4.
Критичне значення c  (0,95) (4) = 9,49 значно менше від фактичного c
(0,95) (4) = 9,49 значно менше від фактичного c  = 96,3, отже, зв’язок між віком подружжя істотний.
= 96,3, отже, зв’язок між віком подружжя істотний.

 ,
, =
= 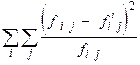 – сума стандартизованих відхилень фактичних частот розподілу від теоретичних; m 1 та m 2 – кількість груп за першою і другою ознаками; n – кількість елементів сукупності.
– сума стандартизованих відхилень фактичних частот розподілу від теоретичних; m 1 та m 2 – кількість груп за першою і другою ознаками; n – кількість елементів сукупності. подано в таблиці 7.13. Теоретичні частоти обчислюють на основі підсумкових частот
подано в таблиці 7.13. Теоретичні частоти обчислюють на основі підсумкових частот  .
. і т. д.
і т. д. .
.


