Теоретическая часть. .
Правила дифференцирования: 1. 2. 3. 4. Производная сложной функции:
Пример 1. Найти производную функции Решение: Пользуясь правилами дифференцирования и таблицей производных, получим:
Воспользуемся формулой производной сложной функции:
Пример 3. Найти производную функции Решение:
Тема: « Условия монотонности функции. Необходимое и достаточное условие экстремума »
Теоретическая часть Пример 1: Пример 2: Найти экстремум функции Найдем производную функции. Она равна Пример 3: Найти точки экстремума и интервалы монотонности функции Находим первую производную:
Тема: « Исследование функции одной переменной и построение графика. Асимптоты графика функции »
|
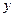
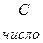
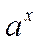
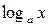
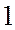
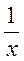
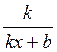
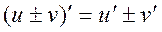
, где С - число
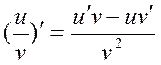
Пример 2. Найти производную функции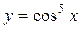 
.
.
.
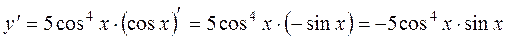. Приравниваем производную к нулю 
и находим критическую точку 
. Чтобы найти ординату этой точки, подставим 
и запишем вершину параболы C(1; 4). Ось симметрии проходит через C параллельно оси 
(рис. 3). Пересечение параболы с осью 
; 
, т.е. A(0; 5). Симметричная ей точка A1(2; 5).
.
и приравниваем ее к нулю 
. Так как 
, то 
и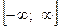 
на два интервала монотонности, 
меняет знак с 
на 
. Следовательно, 
- точка минимума.
