 У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна
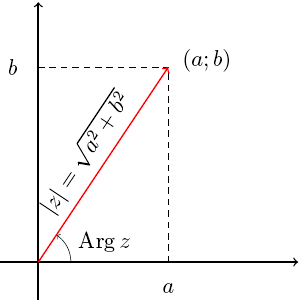
У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна  . Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор. Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ).
. Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор. Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ).
Тригонометрическая форма комплексного числа: 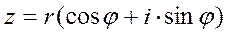 , где
, где 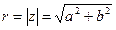 ,
, 
Пример 1: Записать в тригонометрической форме комплексное число 
Решение:
Решение: Найдем 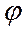 :
:  , откуда
, откуда  , т.к. точка
, т.к. точка 
лежит в третьей четверти.
Учитывая  , имеем:
, имеем: 
Произведение комплексных чисел:
Пример 2: Выполните действие
Частное комплексных чисел:
Пример 3: Выполните действие
Формула Муавра:
Пример 4: Выполните действие
Внимание! Ни в коем случае нельзя использовать четность косинуса, нечетность синуса и проводить дальнейшее «упрощение» записи:

Рассмотрим уравнение  , или, то же самое:
, или, то же самое:  . Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при
. Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при  получается квадратный корень
получается квадратный корень 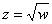
Уравнение вида  имеет ровно
имеет ровно  корней
корней  , которые можно найти по формуле:
, которые можно найти по формуле:
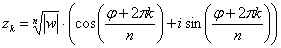 , где
, где  – это модуль комплексного числа
– это модуль комплексного числа  ,
,  – его аргумент, а параметр
– его аргумент, а параметр  принимает значения:
принимает значения: 
Тема: « Вычисление вероятности событий с элементами комбинаторики »

 У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна
У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна  . Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор. Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ).
. Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор. Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ).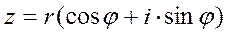 , где
, где 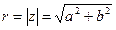 ,
, 

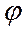 :
:  , откуда
, откуда  , т.к. точка
, т.к. точка 
 , имеем:
, имеем: 







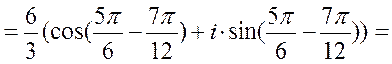





 , или, то же самое:
, или, то же самое:  . Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при
. Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при  получается квадратный корень
получается квадратный корень 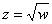
 корней
корней  , которые можно найти по формуле:
, которые можно найти по формуле: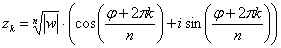 , где
, где  – это модуль комплексного числа
– это модуль комплексного числа  ,
,  – его аргумент, а параметр
– его аргумент, а параметр  принимает значения:
принимает значения: 



