Теоретическая часть. В опыте было получено 30 наблюдений над случайной величиной X, составляющих выборочную совокупность
В опыте было получено 30 наблюдений над случайной величиной X, составляющих выборочную совокупность. Они приведены в таблице. По выборочным данным: 1) составить ряд распределения; найти размах выборки; 2) построить эмпирическую функцию распределения; 3) найти числовые характеристики выборки: 4) Проверить гипотезу Таблица Значения признака Х, полученные из опыта.
Решение 1) Составим ряд распределения: расположим наблюдения Таблица А.
Из этих наблюдений определим наибольшее Хмах = 99 и наименьшее Х мin = 80. Вычислим размах варьирования d=Xmax – Xmin = 99-80=19. 2) Эмпирическая функция распределения Она принимает значения Таким образом, мы имеем
(т.к. значения, меньшие 82, наблюдались два раза).
Построим график эмпирической функции распределения
80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99
3) Найдем числовые характеристики выборочной совокупности Оценка математического ожидания признака Х
Выборочная дисперсия =
Среднеквадратическое отклонение
4) Для проверки гипотезы Если среднее квадратическое отклонение исследуемой случайной величины Х заранее неизвестно (а это та ситуация, в которой мы находимся), то оно оценивается по выборочным данным. В этом случае доверительный интервал имеет вид:
В нашем случае
Получаем доверительный интервал (89,37-2,042(5,27/5,48); 89,37+2,042(5,27/5,48)=(87,41;91,33). Число «90» содержится в построенном доверительном интервале, следовательно, гипотезаH0: М(X)= 90 принимается с уровнем доверия γ=0,95.
|

 в- выборочное среднее, Dв - выборочную дисперсию;
в- выборочное среднее, Dв - выборочную дисперсию;  в- выборочное среднее квадратическое отклонение;
в- выборочное среднее квадратическое отклонение; : математическое ожидание случайной величины Х; М (Х) = 90 против альтернативной гипотезы H
: математическое ожидание случайной величины Х; М (Х) = 90 против альтернативной гипотезы H  : M(X)
: M(X)  (среднее квадратическое отклонение
(среднее квадратическое отклонение  оценивается по выборке). Уровень доверия γ= 0,95.
оценивается по выборке). Уровень доверия γ= 0,95.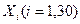 в порядке возрастания в верхней строке таблицы А, в нижней строке nί - количество наблюдений в общем ряду наблюдений.
в порядке возрастания в верхней строке таблицы А, в нижней строке nί - количество наблюдений в общем ряду наблюдений.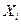
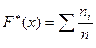 определяет для каждого значения х относительную частоту события Х < x.
определяет для каждого значения х относительную частоту события Х < x. причем
причем  при
при 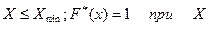 >
> 
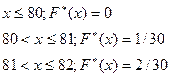
 (т.к. значения меньшие 83, наблюдались 5 раз).
(т.к. значения меньшие 83, наблюдались 5 раз).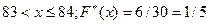
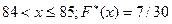

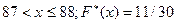

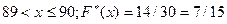












 1
1

 9/10
9/10

 8/10
8/10 7/10
7/10
 6/10
6/10

 5/10
5/10
 4/10
4/10

 3/10
3/10

 2/10
2/10
 1/10
1/10 0
0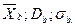


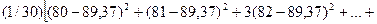


 построим доверительный интервал для математического ожидания случайной величины Х с уровнем доверия γ=0,95.
построим доверительный интервал для математического ожидания случайной величины Х с уровнем доверия γ=0,95. где
где 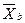 - выборочное среднее; n – объем выборки;
- выборочное среднее; n – объем выборки;  - выборочное среднее квадратическое отклонение по таблице распределения Стьюдента для заданных объема выборки n и уровня доверия γ.
- выборочное среднее квадратическое отклонение по таблице распределения Стьюдента для заданных объема выборки n и уровня доверия γ.




