Схема исследования функций:
· Найти область определения функции.
· Установить, не является ли функция четной, нечетной, периодической.
· Найти точки разрыва и исследовать пределы функции в этих точках.
· Найти точки экстремума и значения функции в этих точках.
· Исследовать интервалы возрастания и убывания функции.
Для исследования функции на возрастание и убывание находят производную ƒ΄(х) функции ƒ(х) определяют ее знак. (Если ƒ΄(х)  0, то ƒ(х) возрастает; если ƒ΄(х)
0, то ƒ(х) возрастает; если ƒ΄(х)  0, то ƒ(х) убывает)
0, то ƒ(х) убывает)
· Найти точки перегиба.
· Исследовать график функции на выпуклость и вогнутость (f ''(x) < 0, то график функции на этом интервале выпуклый, если же f ''(x) > 0 – вогнутый.)
· Найти точки пересечения с осями координат.
· Определить промежутки знакопостоянства функции, т.е. промежутки, на которых ƒ(х)  0 и ƒ(х)
0 и ƒ(х)  0.
0.
· Построить график заданной функции.
Пример 1. Исследовать функцию у =  и построить ее график. Решение. Область определения функции – вся числовая ось, кроме точки х = 1, поэтому, D(у) = (-
и построить ее график. Решение. Область определения функции – вся числовая ось, кроме точки х = 1, поэтому, D(у) = (-  1)
1)  (1; +
(1; +  ). * Так как у (-х) =
). * Так как у (-х) =  = -
= -  , то функция ни четная и ни нечетная. * Так как у(х + Т) =
, то функция ни четная и ни нечетная. * Так как у(х + Т) =  =
=  ни при каком Т
ни при каком Т  0, то данная функция не периодическая. * Строим прямую х = 1. В случае, когда х приближается к 1 слева, значения функции стремятся к –
0, то данная функция не периодическая. * Строим прямую х = 1. В случае, когда х приближается к 1 слева, значения функции стремятся к –  , а в случае, когда х приближается к 1 справа, значения функции стремятся к +
, а в случае, когда х приближается к 1 справа, значения функции стремятся к +  . Так как у =
. Так как у =  +
+  = х + 1 +
= х + 1 +  , то при |х|
, то при |х|  график этой функции приближается к графику функции у1 = х +1. * Находим производную у΄ =
график этой функции приближается к графику функции у1 = х +1. * Находим производную у΄ =  =
= 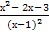 и из уравнения
и из уравнения  - 2х – 3 = 0 определяем критические точки: х1 = - 1 и х2 = 3. Так как для точек интервала (-
- 2х – 3 = 0 определяем критические точки: х1 = - 1 и х2 = 3. Так как для точек интервала (-  ; - 1) производная имеет знак «+», а для точек интервала (- 1; 1) производная имеет знак «-», то точка х1 = -1 является точкой максимума функции. Аналогично убеждаемся, что точка х2 = 3 является точкой минимума функции. * Так как уравнение х2 + 3 = 0 не имеет действительных корней, то график функции не пересекает ось 0х. * На интервале (-
; - 1) производная имеет знак «+», а для точек интервала (- 1; 1) производная имеет знак «-», то точка х1 = -1 является точкой максимума функции. Аналогично убеждаемся, что точка х2 = 3 является точкой минимума функции. * Так как уравнение х2 + 3 = 0 не имеет действительных корней, то график функции не пересекает ось 0х. * На интервале (-  ; - 1) функция возрастает, на интервале (- 1; 1) – убывает, на интервале (1; 3) вновь убывает, на интервале (3; +
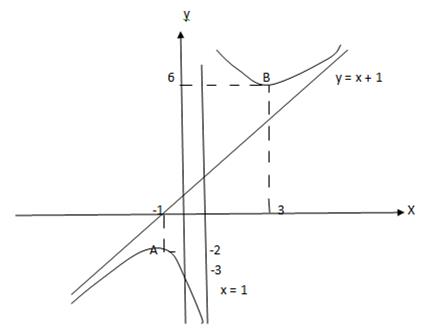
; - 1) функция возрастает, на интервале (- 1; 1) – убывает, на интервале (1; 3) вновь убывает, на интервале (3; +  ) – возрастает. Найдем точки графика при х1 = - 1 и х2 = 3; А (- 1; - 2); В (3; 6). * Найдем точки пересечения графика функции с осью 0у: у(0) = - 3. * Построим график исходной функции.
) – возрастает. Найдем точки графика при х1 = - 1 и х2 = 3; А (- 1; - 2); В (3; 6). * Найдем точки пересечения графика функции с осью 0у: у(0) = - 3. * Построим график исходной функции.
Тема: « Вычисление неопределенных интегралов »

 0, то ƒ(х) возрастает; если ƒ΄(х)
0, то ƒ(х) возрастает; если ƒ΄(х)  0, то ƒ(х) убывает)
0, то ƒ(х) убывает) и построить ее график. Решение. Область определения функции – вся числовая ось, кроме точки х = 1, поэтому, D(у) = (-
и построить ее график. Решение. Область определения функции – вся числовая ось, кроме точки х = 1, поэтому, D(у) = (-  1)
1)  (1; +
(1; +  ). * Так как у (-х) =
). * Так как у (-х) =  = -
= -  =
=  ни при каком Т
ни при каком Т  0, то данная функция не периодическая. * Строим прямую х = 1. В случае, когда х приближается к 1 слева, значения функции стремятся к –
0, то данная функция не периодическая. * Строим прямую х = 1. В случае, когда х приближается к 1 слева, значения функции стремятся к –  +
+  = х + 1 +
= х + 1 +  график этой функции приближается к графику функции у1 = х +1. * Находим производную у΄ =
график этой функции приближается к графику функции у1 = х +1. * Находим производную у΄ =  =
= 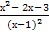 и из уравнения
и из уравнения  - 2х – 3 = 0 определяем критические точки: х1 = - 1 и х2 = 3. Так как для точек интервала (-
- 2х – 3 = 0 определяем критические точки: х1 = - 1 и х2 = 3. Так как для точек интервала (- 



