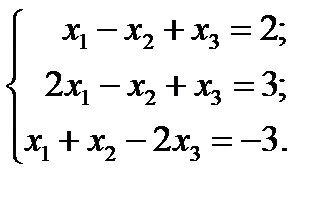Проверка
Пример 11.2. Определить, при каких значениях λ существует матрица обратная данной:
Решение: Всякая невырожденная матрица имеет обратную. Вычислим детерминант матрицы A:
Если 4λ – 9 ≠ 0, т. е. Пример 11.3. Показать, что матрица A является обратной для B, если
Решение: Найдём произведение матриц A и B:
Аналогично A × B = E. Следовательно, матрица A является обратной для B. [kgl]. [gl] Тема 12. Численные методы решения систем линейных алгебраических уравнений. Формулы Крамера [:] Метод Крамера (правило Крамера) – способ решения квадратных систем линейных алгебраических уравнений с ненулевым детерминантом основной матрицы (причём для таких систем решение существует и оно единственное). Описание метода. Для системы n линейных уравнений с n неизвестными (над произвольным полем)
Основная матрица A такой системы квадратная. Детерминант этой матрицы
называется детерминантом системы. Если детерминант системы отличен от нуля, то система называется невырожденной, и решение записывается в виде
где
(i -й столбец матрицы системы заменяется столбцом свободных членов). Схема главного детерминанта системы и последовательной замены его столбцов столбцом свободных членов показана на рисунке 12.1 для n = 3.
Рисунок 12.1 – Схема главного детерминанта и формирование вспомогательных детерминантов путём замены его столбцов столбцом свободных членов: a) главный детерминант со столбцом свободных членов; b), c) и d) формирование вспомогательных детерминантов
Пусть дана система линейных уравнений с двумя неизвестными:
Если главный детерминант системы отличен от нуля, то система имеет решение, притом единственное. Решение системы определяется формулами
где x 1, x 2 – корни системы уравнений; в Δ – главный детерминант системы; Δ x 1, Δ x 2 – вспомогательные детерминанты. Главный детерминант системы вычисляется по схеме:
Вспомогательные детерминанты:
Пример 12.1. Решить систему линейных уравнений
Решение:
Значит, Пример 12.2. Решить систему линейных уравнений
Решение: Вычисляем главный детерминант системы
Главный детерминант отличен от нуля, следовательно, система имеет единственное решение. Вычисляем вспомогательные детерминанты системы. Для этого последовательно заменяем столбцы матрицы системы столбцом свободных членов. Далее по формулам
Ответ:
[kgl].
[gl] Тема 13. Решение системы матричным способом [:]
Матричный метод решения систем линейных алгебраических уравнений с ненулевым детерминантом состоит в следующем. Пусть дана система n линейных уравнений с n неизвестными:
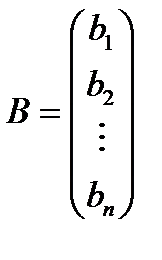
Матрица, состоящая из коэффициентов при неизвестных, т. е. матрица
называется матрицей системы, а матрица-столбец, составленная из величин b 1, b 2, …, bn
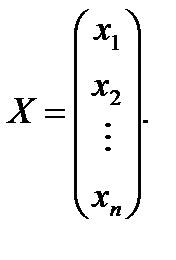
называется столбцом свободных членов. Составим ещё матрицу-столбец неизвестных
Тогда систему (13.1) можно записать в матричной форме:
Если det A ≠ 0, то умножая это матричное уравнение слева на A –1 – матрицу, обратную матрице A, получим: A –1 ·(A · X) = A –1· B. Тогда A –1· A = E (учитывая ассоциативность матричного произведения), получаем X = A –1· B. (13.3) Правая часть этого уравнения даёст столбец решений исходной системы. На этой формуле основан матричный способ решения систем линейных уравнений. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равных числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю детерминанта матрицы A: det A ≠ 0. Пример 13.1. Решить матричным способом систему линейных уравнений
Решение. Для данной системы
Чтобы воспользоваться формулой (13.3), надо найти матрицу, обратную к матрице A. В примере 11.1 показано, что матрица A –1 имеет вид (11.2). Подставляя в (13.3), имеем:
Ответ: x 1 = 2; x 2 = –1; x 3 = –3.
[kgl].
[gl] Тема 14. Решение системы методом Гаусса (метод исключения неизвестных) [:]
Одним из наиболее универсальных и эффективных методов решения систем линейных алгебраических уравнений является метод Гаусса, состоящий в последовательном исключении неизвестных. Пусть дана система уравнений
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду. Приведённая ниже система имеет ступенчатый вид
где На втором этапе (обратный ход) идёт последовательное определение неизвестных из этой ступенчатой системы. Опишем метод Гаусса подробнее. Прямой ход. Будем считать, что элемент a 11 ≠ 0 (если a 11 = 0, то первым в системе запишем уравнение, в котором коэффициент при x 1 отличен от нуля). Преобразуем систему (14.1), исключив неизвестное x 1 во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на
Здесь Аналогичным образом, считая главным элементом Если в процессе приведения системы (14.1) к ступенчатому виду появятся нулевые уравнения, т. е. равенства вида 0 = 0, их отбрасывают. Если же появится уравнение вида 0 = bi, а bi ≠ 0, то это свидетельствует о несовместности системы. Второй этап (обратный ход) заключается в решении ступенчатой системы. Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное xk через остальные неизвестные (xk +1, …, xn). Затем подставляем значение xk в предпоследнее уравнение системы и выражаем xk – 1 через (xk +1, …, xn); затем находим xk – 2, …, x 1. Придавая свободным неизвестным (xk +1, …, xn) произвольные значения, получим бесчисленное множество решений системы. Замечания: 1. Если ступенчатая система оказывается треугольной, т. е. k = n, то исходная система имеет единственное решение. Из последнего уравнения находим xn, из предпоследнего уравнения – xn – 1, далее поднимаясь по системе вверх, найдём все остальные неизвестные (xn – 2, …, x 1). 2. На практике удобнее работать не с системой (14.1), а с расширенной её матрицей, выполняя все элементарные преобразования над её строками. Удобно, чтобы коэффициент a 11 был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на a 11 ≠ 1).
Пример 13.1. Решить методом Гаусса систему линейных уравнений.
|

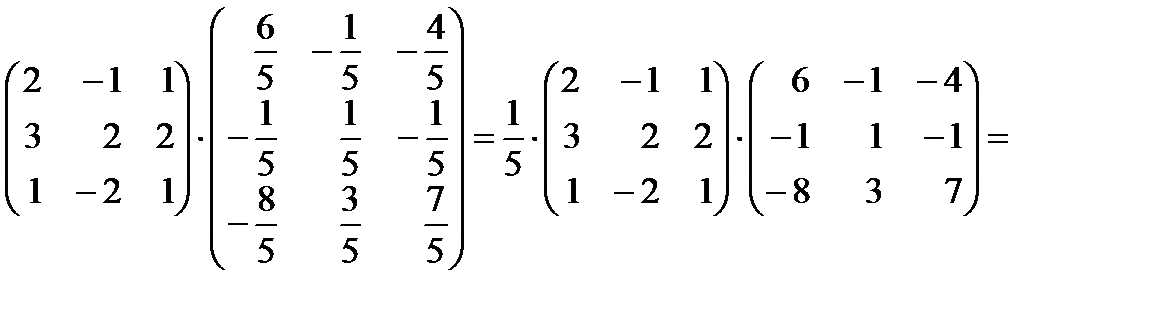
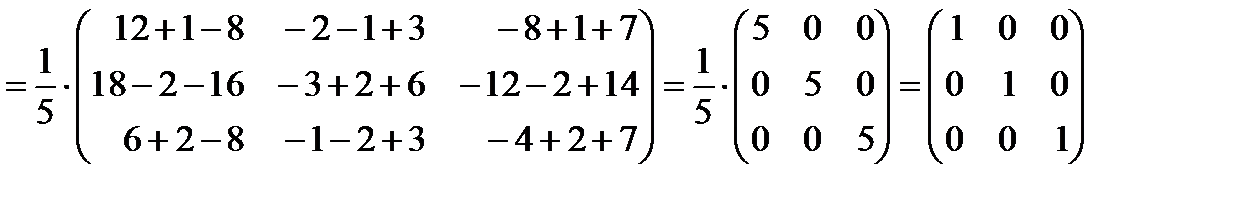 .
. .
.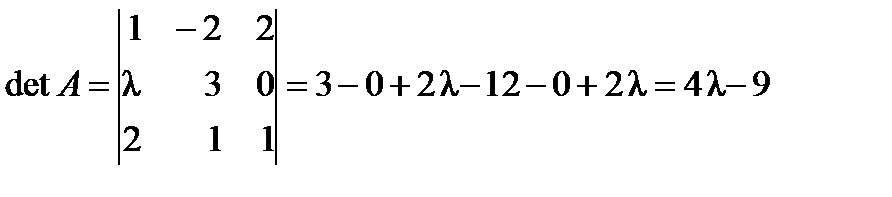 .
.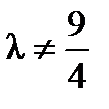 , то det A ≠ 0, т. е. матрица A невырожденная, имеет обратную матрицу A –1.
, то det A ≠ 0, т. е. матрица A невырожденная, имеет обратную матрицу A –1.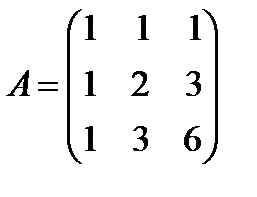 ,
, 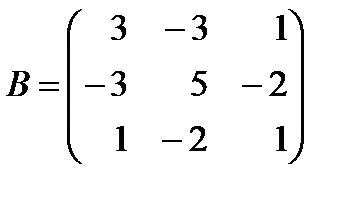 .
.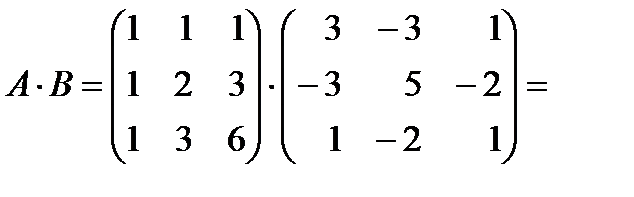
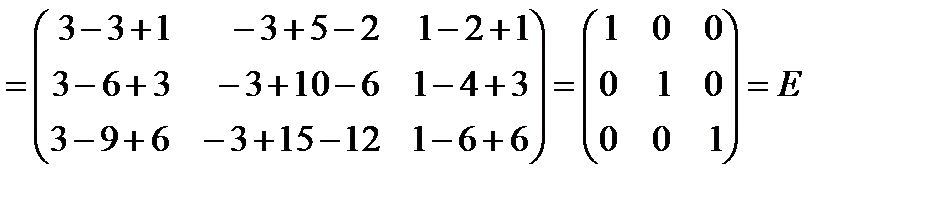 .
.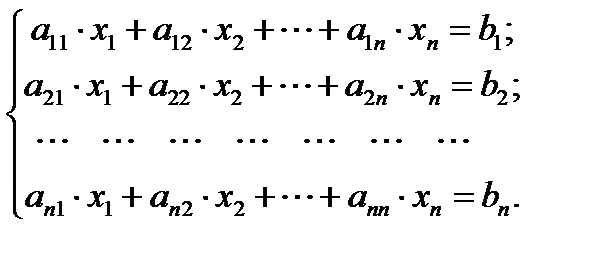
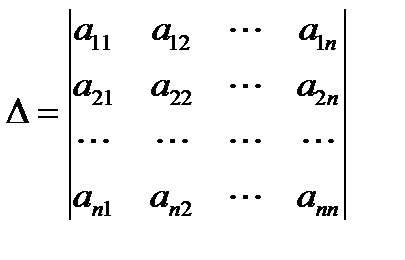
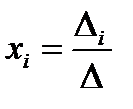 ,
,
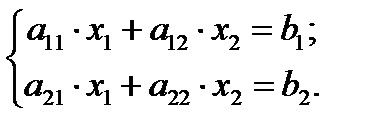
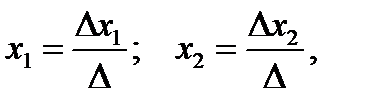
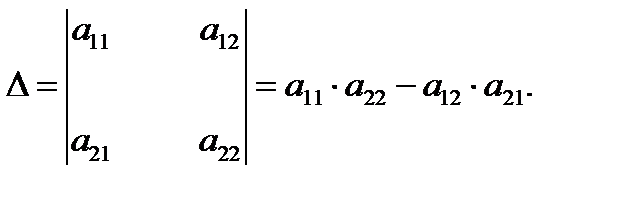

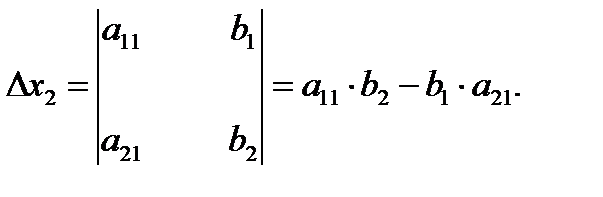

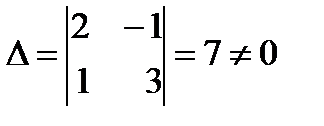 ,
, 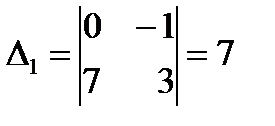 ,
, 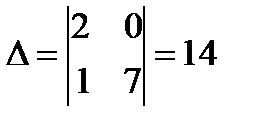 .
.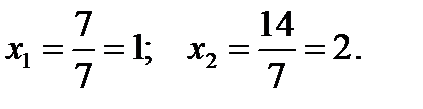
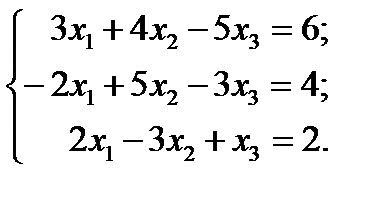
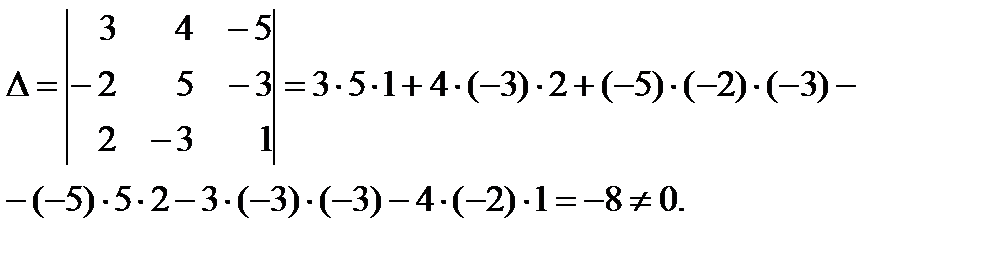
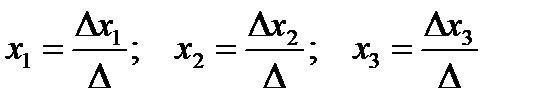 находим решение.
находим решение.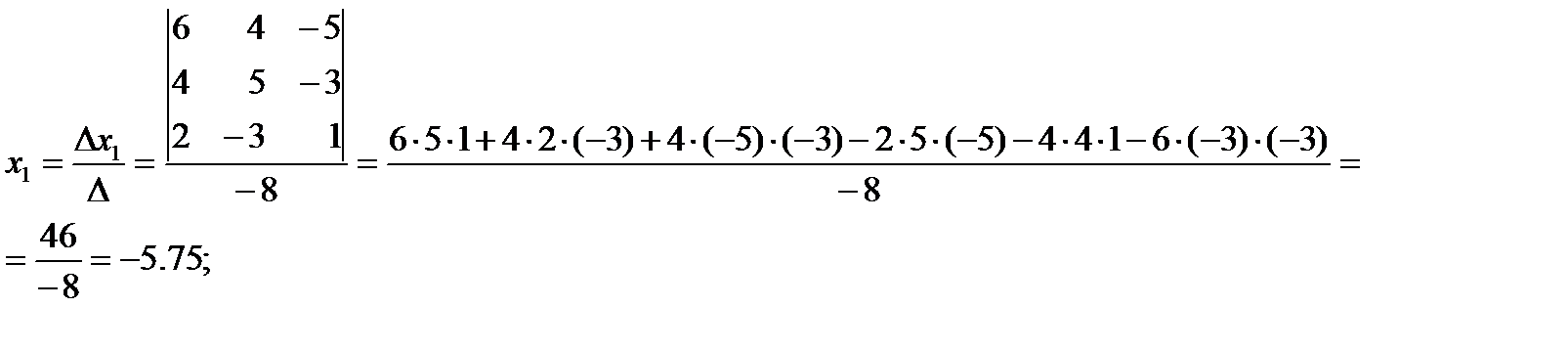
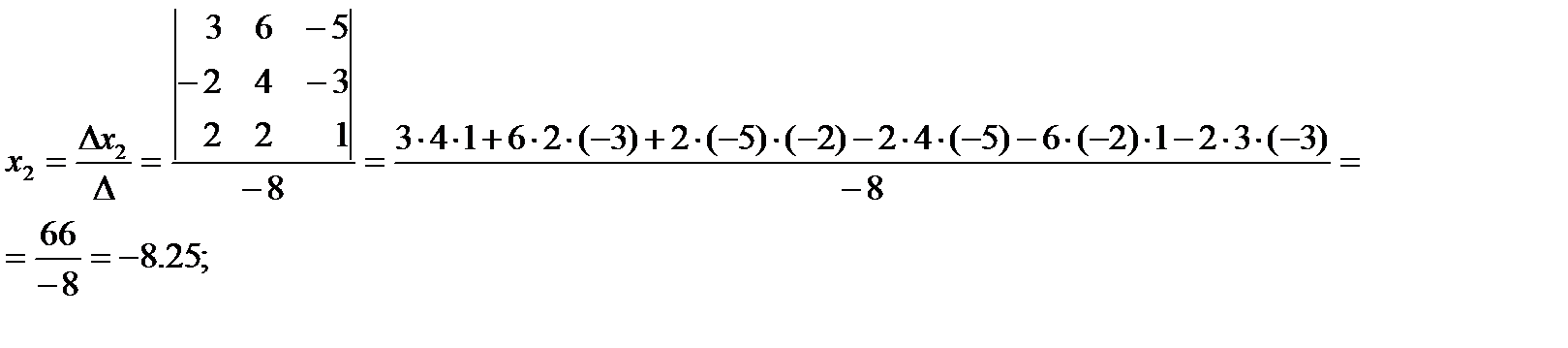

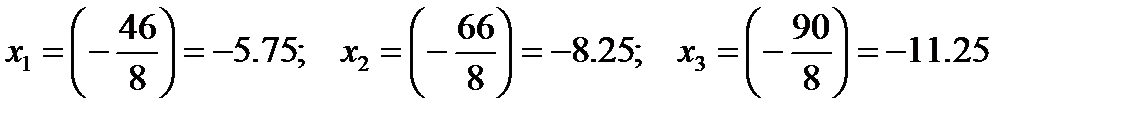 .
.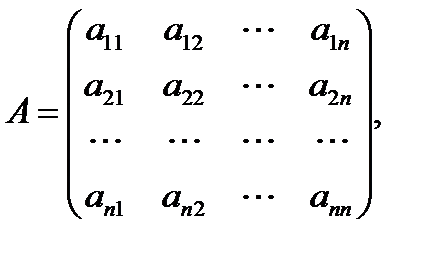
 ,
,
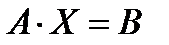 .
.
 .
.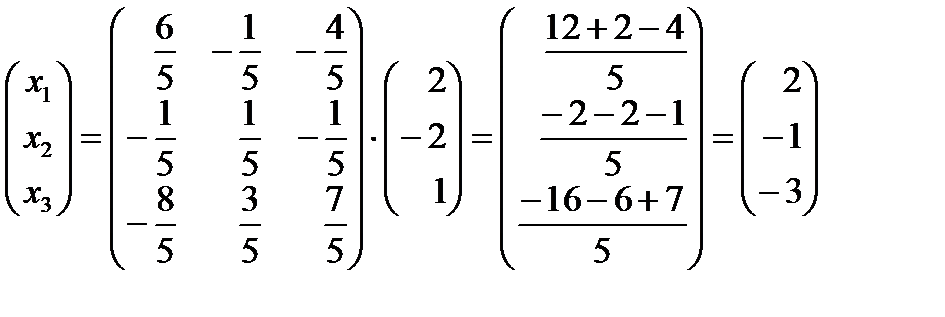 .
.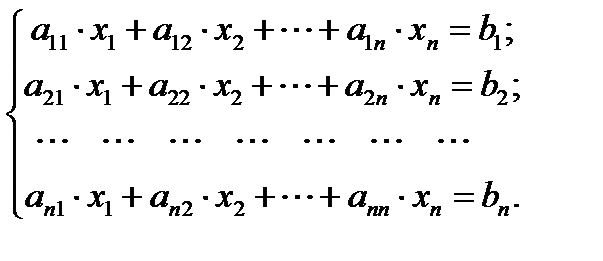 (14.1)
(14.1)
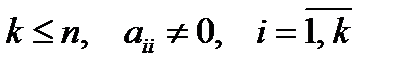 . Коэффициенты aij называются главными элементами системы.
. Коэффициенты aij называются главными элементами системы. и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на
и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на  и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему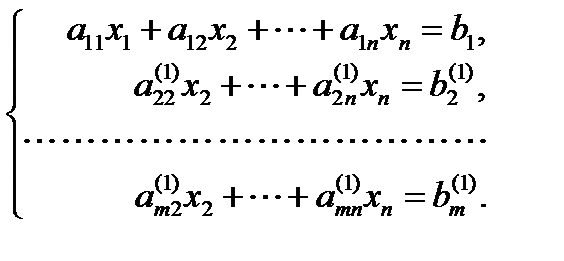
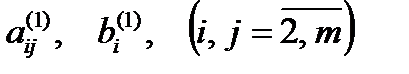 – новые значения коэффициентов и правых частей, которые получаются после первого шага.
– новые значения коэффициентов и правых частей, которые получаются после первого шага.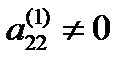 , исключим неизвестное x 2 из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока это возможно.
, исключим неизвестное x 2 из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока это возможно.