Решение. Зная пределы интегрирования, a = 1 и b = 9, находим шаг
Зная пределы интегрирования, a = 1 и b = 9, находим шаг
Тогда точками разбиения будут
Значения подынтегральной функции
Найдём численное значение интеграла по формуле левых прямоугольников:
По формуле правых прямоугольников:
Пример 15.2. По методу левых прямоугольников вычислить определённый интеграл
Пример 15.3. По методу правых прямоугольников вычислить определённый интеграл
Пример 15.4. По методу средних прямоугольников вычислить определённый интеграл
Для решения задач по схеме алгоритма составить программу.
[kgl].
[gl] Тема 16. Метод трапеций. Схема алгоритма метода трапеций [:]
Формула трапеций имеет следующий вид
Эта формула означает, что площадь криволинейной трапеции заменяется площадью многоугольника, составленного из n трапеций (рисунок 16.1), при этом кривая заменяется вписанной в неё ломаной. Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной. Разобьём отрезок [ a, b ] на n равных частей длины Заменим кривую y = f (x) ломаной линией, звенья которой соединяют концы ординат yi и yi +1 (i = 0, 1, 2, …, n). Тогда площадь криволинейной трапеции приближённо равна сумме площадей обычных трапеций с основаниями yi и yi +1 высотой
или
Рисунок 16.1 – К приближённому вычислению интеграла методом трапеций Пример 16.1. Пользуясь формулой трапеций вычислить определённый интеграл
|

 .
. .
.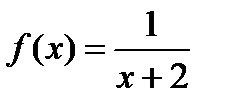 в этих точках таковы
в этих точках таковы .
.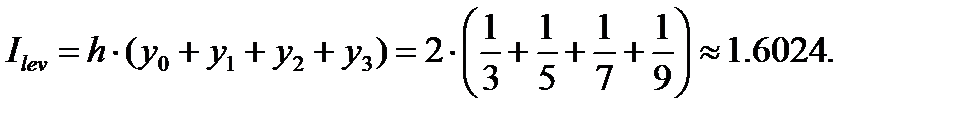

 .
. .
. .
. . (16.1)
. (16.1)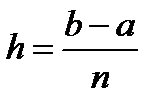 . Абсциссы точек деления a = x 0, x 1, x 2, …, b = xn (рисунок 16.1). Пусть y 0, y 1, …, yn – соответствующие им ординаты графика функции. Тогда расчётные формулы для этих значений примут вид
. Абсциссы точек деления a = x 0, x 1, x 2, …, b = xn (рисунок 16.1). Пусть y 0, y 1, …, yn – соответствующие им ординаты графика функции. Тогда расчётные формулы для этих значений примут вид  .
. :
:
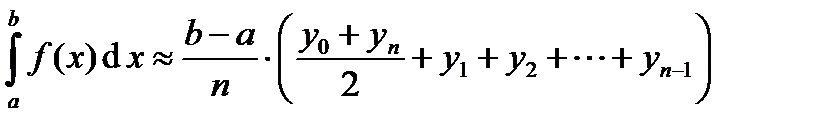 .
. при n = 4.
при n = 4.


