Решение. N = 0, 1, 2 (три узла интерполяции).
N = 0, 1, 2 (три узла интерполяции).
– уравнение параболы, проходящей через точки (x 0, y 0), (x 1, y 1), (x 2, y 2);
Построим график этой функции (рисунок 18.1) и отметим узловые точки Mi (xi, yi). Это квадратичная парабола с вертикальной осью симметрии. Её график проходит через три заданные точки.
Рисунок 18.1 – График полученной функции [kgl].
[gl] Тема 19. Числовые ряды. Частные суммы. Вычисление суммы рядов. Схема алгоритма вычисления суммы [:]
Ряды играют исключительную роль в математике как очень эффективное средство математического исследования и моделирования. Известные всем таблицы тригонометрических функций, таблицы логарифмов и т. п. составляются с помощью рядов для этих функций. Точное значение числа π также получается с помощью ряда. Понятие суммы конечного числа чисел и свойства суммы были известны уже в древнейшие времена. С частными примерами сумм бесконечных рядов, например, с суммой членов убывающей геометрической прогрессии, математики имели дело уже во времена Архимеда. Успешно пользовались рядами Ньютон, Ляйбниц, Эйлер, Гаусс. Однако точная теория рядов, основанная на понятии предела последовательности и содержащая доказательства основных теорем, была построена в первой половине XIX в. в основном Коши. С тех пор ряды стали незаменимым средством для математики, появились разделы математики, например, теория аналитических фунций, целиком основанные на теории рядов. Сумма членов бесконечной числовой последовательности u 1, u 2, …, un, … называется числовым рядом.
при этом числа u 1, u 2, … будем называть членами ряда, а un – общим членом ряда. Суммы
Таким образом, возможно рассматривать последовательности частичных сумм ряда Так как S есть предел последовательности Sn, то очевидно:
Поэтому, взяв достаточно большое число членов сходящегося ряда, сумму этого ряда можно вычислить с необходимой степенью точности. Для сходящегося ряда его n –й член un при неограниченном возрастании номера n стремится к нулю, т. е. Ряд
Если последовательность частных сумм ряда расходится, т. е. не имеет предела или имеет бесконечный предел, то ряд называется расходящимся и ему неставят в соответствие никакой суммы. Если ряд Суммой или разностью этих рядов будет называться ряд Если ряды
Разность двух сходящихся рядов также будет сходящимся рядом.
Пример 19.1. С помощью радикального признака Коши исследовать ряд
|


 .
. ,
, называются частичными (частными, парциальными) суммами ряда
называются частичными (частными, парциальными) суммами ряда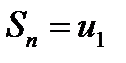 ,
,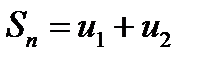 ,
, ,
,

 . При этом разность между суммой S и частичной суммой Sn называется n -м остатком ряда Rn = S – Sn.
. При этом разность между суммой S и частичной суммой Sn называется n -м остатком ряда Rn = S – Sn. .
.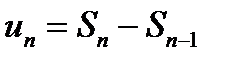 ;
;  .
. .
. сходится и его сумма равна S, то ряд
сходится и его сумма равна S, то ряд 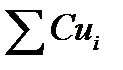 тоже сходится, и его сумма равна CS (C ≠ 0).
тоже сходится, и его сумма равна CS (C ≠ 0). , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами. и
и  сходятся и их суммы равны соответственно S и σ, то ряд
сходятся и их суммы равны соответственно S и σ, то ряд 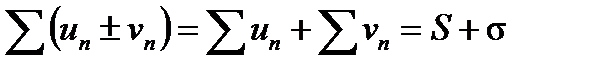
 на сходимость.
на сходимость.


