Решение. Вычисление суммы ряда с заданной точностью ε следует производить до тех пор, пока не выполнится условие
Вычисление суммы ряда с заданной точностью ε следует производить до тех пор, пока не выполнится условие | un | ≤ ε. В данном примере вычисление суммы ряда
необходимо производить до тех пор, пока очередной член ряда по абсолютной величине не будет меньше ε = 0.001. Обозначим n –й член ряда через
Тогда алгоритм нахождения суммы ряда будет иметь вид: y = y + U. При составлении программы определяем последующий член ряда через предыдущий:
Схема алгоритма вычисления суммы ряда приведена на рисунке 19.1.
Рисунок 19.1 – Схема алгоритма вычисления суммы ряда
[kgl].
[gl] Тема 20. Разложение функций в степенные ряды. Приближённые вычисления значений функции с помощью степенных рядов [:]
Степенные ряды широко используются в теоретических исследованиях и в приближённых вычислениях. Для приложений важно уметь данную функцию f (x) разлагать в степенной ряд, т. е. функцию f (x) представлять в виде суммы степенного ряда. Как известно, для любой функции f (x), определённой в окрестности точки x 0 и имеющей в ней производные до (n + 1)-го порядка включительно, справедлива формула Тейлора:
где
где Если функция f (x) имеет производные любых порядков в окрестности точки x 0 и остаточный член Rn (x) стремится к нулю при
Если в ряде Тейлора положить x 0 = 0, то получим разложение функции по степеням x в так называемый ряд Маклорена:
Пусть для функции f (x) составлен соответствующий ряд Тейлора. Для того, чтобы ряд Тейлора (20.2) функции f (x) сходился к f (x) в точке x, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (20.1) стремился к нулю при n → ∞, т. е. чтобы Разложение некоторых элементарных функций в ряд Тейлора (Маклорена) Для разложения функции f (x) в ряд Маклорена (20.3) нужно: a) найти производные b) вычислить значения производных в точке x 0 = 0; c) написать ряд (20.3) для заданной функции и найти его интервал сходимости; d) найти интервал (– R; R), в котором остаточный член ряда Маклорена Rn (x) → 0 при n → ∞. Если такой интервал существует, то в нём функция f (x) и сумма ряда Маклорена совпадают. Приведём таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций
Докажем формулу (20.4). Пусть f (x) = ex. Имеем: a) b) c) d) для всех Докажем формулу (20.5). Пусть f (x) = sin x. Имеем: a) b) c) d) Любая производная функции f (x) = sin x по модулю не превосходит единицы, Докажем формулу (20.6). Пусть f (x) = cos x. Проще получить разложение функции cos x, воспользовавшись свойством, что степенной ряд внутри интервала сходимости можно почленно дифференцировать. После этого получим:
|


 .
. , при этом
, при этом  .
. , (20.1)
, (20.1) , – остаточный член в форме Лагранжа. Формулу (20.1) кратко можно записать в виде
, – остаточный член в форме Лагранжа. Формулу (20.1) кратко можно записать в виде ,
, – полином Тейлора.
– полином Тейлора.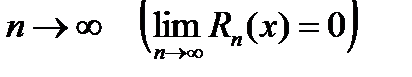 , то из формулы Тейлора получается разложение функции f (x) по степеням (x – x 0), называемое рядом Тейлора:
, то из формулы Тейлора получается разложение функции f (x) по степеням (x – x 0), называемое рядом Тейлора: . (20.2)
. (20.2)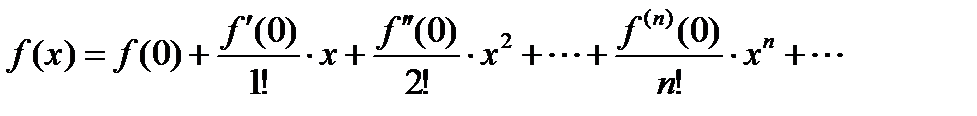 (20.3)
(20.3) .
.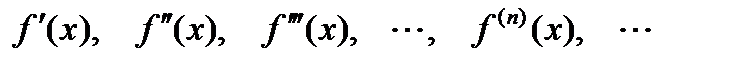 ;
;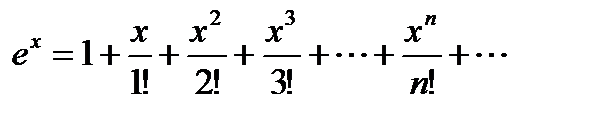 ,
,  , (20.4)
, (20.4) ,
,  ,
,  ,
, (20.7)
(20.7) ,
,  , (20.8)
, (20.8) ,
,  ,
,  ,
,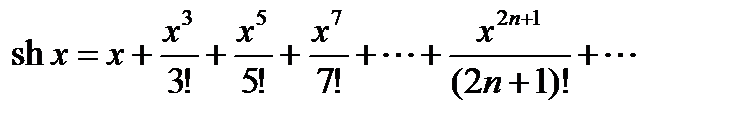 ,
, 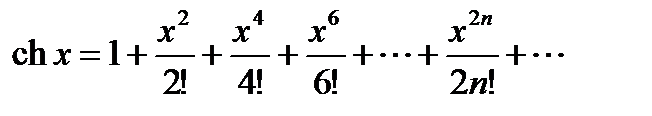 ,
,  ;
; ;
; , т. е. ряд сходится в интервале
, т. е. ряд сходится в интервале  ;
; имеем
имеем  , т. е. все производные в этом интервале ограничены одним и тем же числом M = eR. Следовательно,
, т. е. все производные в этом интервале ограничены одним и тем же числом M = eR. Следовательно,  .
.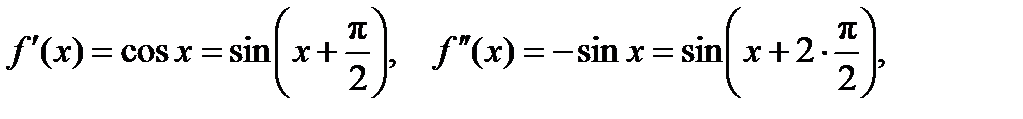
 ;
;
 . Следовательно, имеет место разложение (20.5).
. Следовательно, имеет место разложение (20.5).


