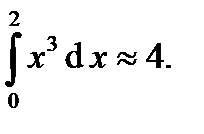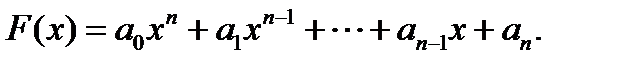Решение. .
Имеем: f (x) = x 3,
a) по формуле прямоугольников:
т. е. b) по формуле трапеций:
т. е. c) по формуле парабол:
Точное значение интеграла Абсолютные погрешности соответствующих формул таковы: a) 0.125; b) 0.25; c) 0.
[kgl].
[gl] Тема 18. Интерполяция и экстраполяция. Интерполяционный полином Лагранжа [:]
Интерполяция – способ нахождения промежуточых значений величины по имеющемуся дискретному набору известных значений. В научных и инженерных расчётах часто приходится оперировать наборами значений, полученных экспериментальным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Например, известны некоторые значения функции – физической величины, замеренные через один час. Необходимо найти значения в промежутках через 30 мин. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных. Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, т. е. интерполировать, более простую функцию. Разумеется, использование упрщённой функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция, но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах. Наиболее часто встречающимся видом точечной аппроксимации является интерполяция. Пусть задан дискретный набор точек xi (i = 0, 1, …, n), называемых узлами интерполяции, причём среди этих точек нет совпадающих, а также значения функции yi в этих точках. Требуется построить функцию g (x), проходящую через все заданные узлы. Таким образом, критерием близости функции является g (xi) = yi. В качестве функции g (x) обычно выбирается полином, который называют интерполяционным полиномом. В том случае, если полином един для всей области интерполяции, говорят, что интерполяция глобальная. В тех случаях, когда между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции. Найдя интерполяционный полином, можно вычислить значения функции f (x) между узлами (провести интерполяцию в узком смысле слова), а также определить значение функции f (x) даже за пределами заданного интервала (провести экстраполяцию). Пусть имеется n значений xi, каждому из которых соответствует своё значение yi. Требуется найти такую функцию F, что:
При этом: · xi называют узлами интерполяции; · пары (xi, yi) называют точками данных; · разницу между соседними значениями (xi – xi – 1) называют шагом; · функцию F (x) – интерполирующей функцией или интерполянтом. Задача интерполирования состоит в том, чтобы по значениям функции в некоторых точках восстановить её значения в остальных точках отрезка. Функция F называется интерполирующей, точки x 0, x 1, x 2, …, xn – узлами интерполяции. Будем искать функцию F в виде полинома степени n:
Можно найти коэффициенты ai, i = 0, 1, 2, …, n, при этом получим систему из (n + 1) уравнений с (n + 1) неизвестными
Эта система имеет единственное решение, так как по нашему предположению все xi различны. Решая эту систему относительно неизвестных a 0, a 1, a 2, …, an, получим аналитическое выражение полинома. Описанный приём можно использовать при решении задач интерполирования, но на практике используют другие более удобные и менее трудоёмкие методы.
|

 ,
,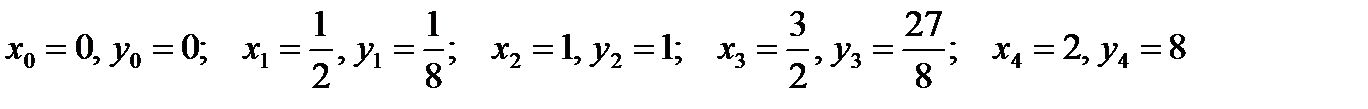 ;
;


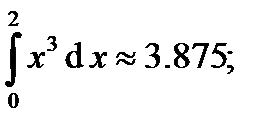


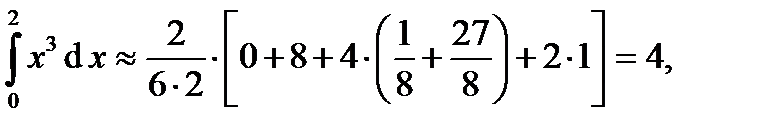 т. е.
т. е.